Задача 183 Найдите значение выражения tg(Pi/3)/cos...
Условие
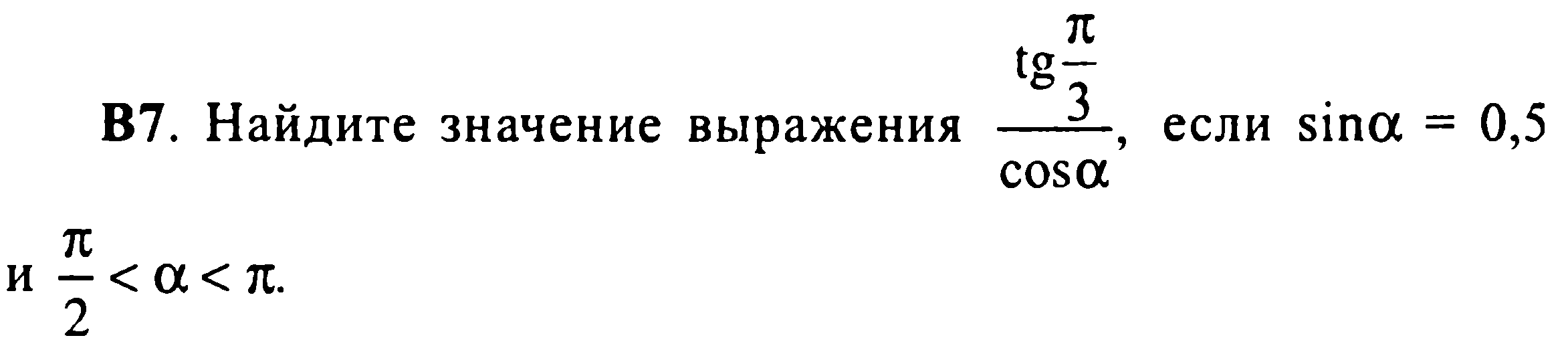
математика 10-11 класс
5224
Решение
И, конечно, прежде всего мы при этом должны помнить об основном тригонометрическом тождестве sin^2x + cos^2x = 1. Очень важно при этом понимать, что, зная sina, мы можем найти не cosa, а cos^2a. Поэтому для нахождения cosa нужна дополнительная информация. Она дана в условии Pi/2 < a < Pi, которое позволяет определить знак cosa, в данном случае отрицательный.
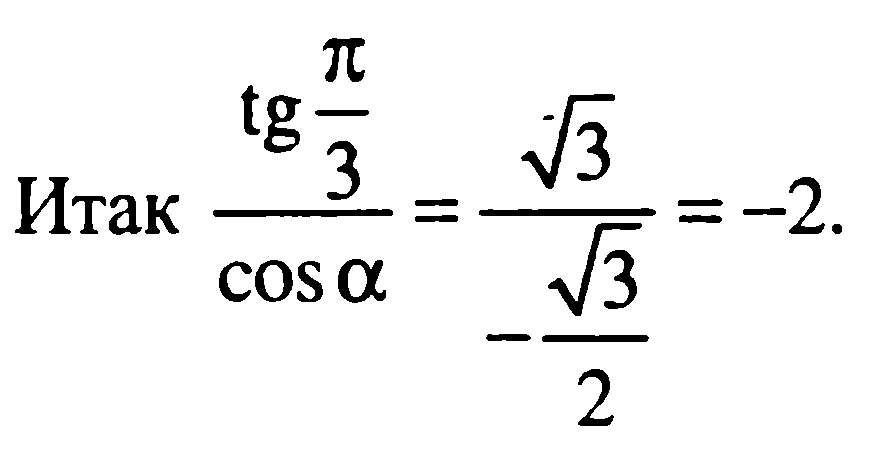
Ответ: -2