Задача 18255 ОГЭ-26) На стороне ВС остроугольного...

slava191

14.10.2017

ОГЭ-26) На стороне ВС остроугольного треугольника АВС как на диаметре построена полуокружность, пересекающая высоту AD в точке М , AD = 9, MD = 6 , Н — точка пересечения высот треугольника АВС. Найдите АН.

SOVA

14.10.2017

★

Проведем высоту BE, ∠ BEC=90 градусов, ВС- диаметр,
∠ BEC опирается на диаметр ВС.
Значит точка Е - точка пересечения полуокружности с диаметром ВС и стороны АС.

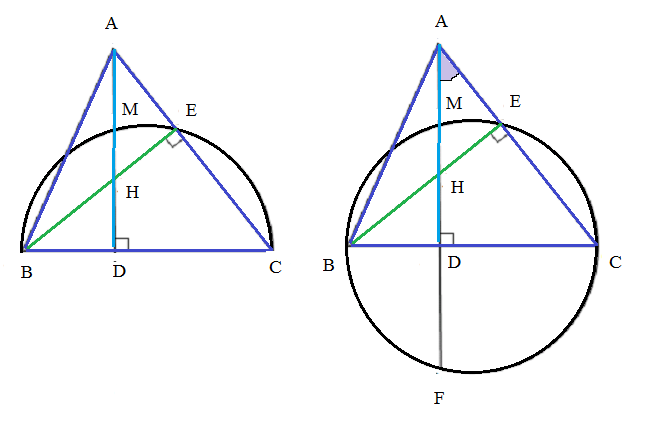
Достроим полуокружность до окружности и продолжим высоту AD до пересечения с окружностью,
получим точку F.

По условию AD=9, MD=6
Значит АМ=AD-MD= 9 - 6 = 3

MD = DF = 6
AF = AD+DF= 9+6=15

По свойству секущих
AM*AF=AE*AC

AM*AF=3*15

Значит и AE*AC=45

Δ AНЕ и Δ ADC подобны как прямоугольные треугольники, имеющие общий острый угол ∠ DAC.

Из подобия

AH:AC=AE:AD ⇒ AH = AE* AC/AD= 45/9 = 5

О т в е т. АН=5