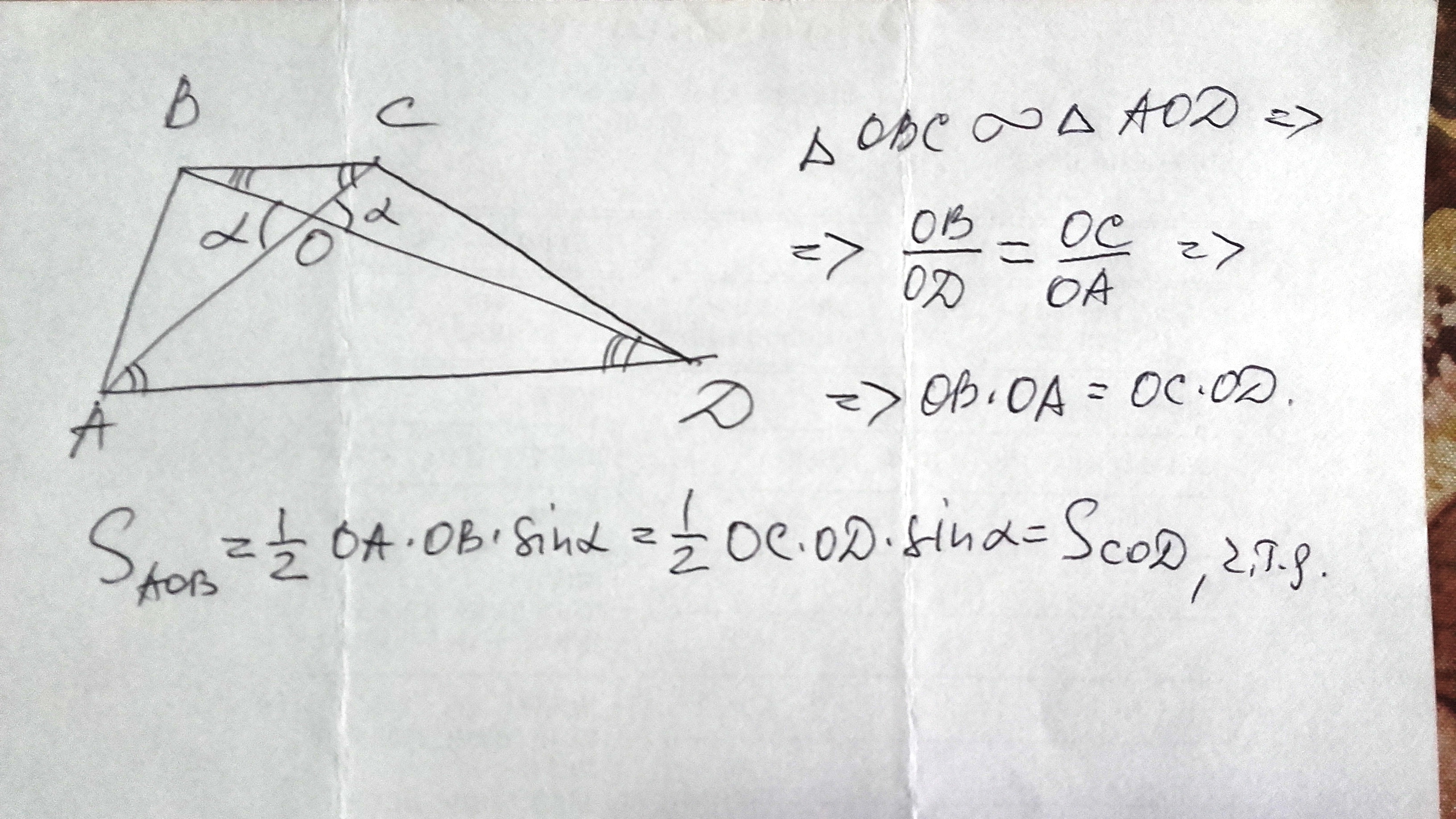
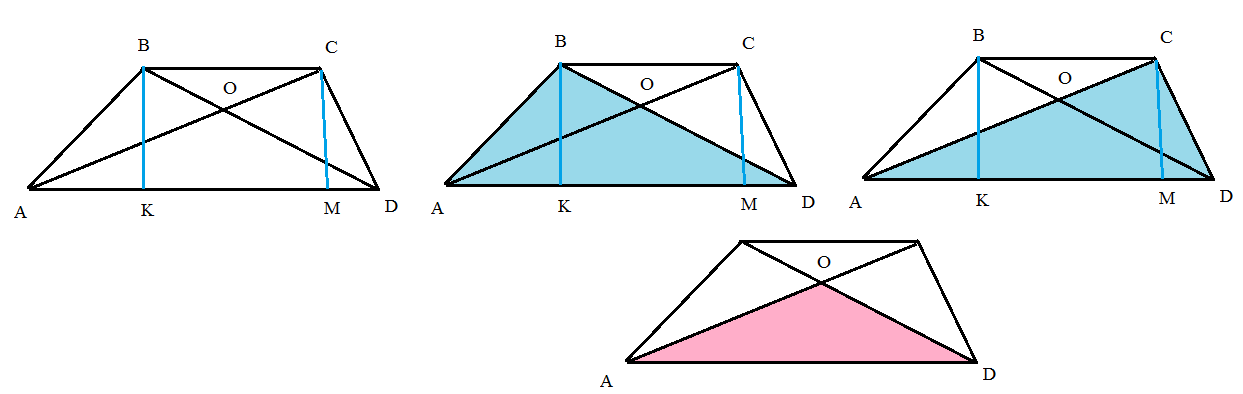
Задача 18254 В трапеции ABCD с основаниями AD и ВС...

slava191

14.10.2017

В трапеции ABCD с основаниями AD и ВС диагонали пересекаются в точке О. Докажите, что площади треугольников АОВ и COD равны.

SOVA

15.10.2017

★

Проведем высоты BK и СM.
BK=CM=h

S( Δ ABD)=(1/2)AD*h
S( Δ ACD)=(1/2)AD*h

S( Δ ABD)=S( Δ ACD)

Так как

S(Δ ABD)=S(Δ ABО)+S(Δ AОD) ⇒ S(Δ ABО)=S(Δ ABD)-S(Δ AОD)

S( Δ ACD)=S( Δ СОD)+S( Δ AОD) ⇒ S(Δ CОD)=S(Δ ACD)-S(Δ AОD)

Правые части равны, значит равны и левые.

S( Δ AOB)=S( Δ COD)

u859314469

15.10.2017

По моему так гораздо проще и понятней. Вопросы и комментарии 495-720-0951 или prois@mai.ru Елена Викторовна