Задача 18245 В нескольких эстафетах, которые...
Условие
При подведении итогов баллы каждой команды по всем эстафетам суммируются. Побеждает команда, набравшая наибольшее количество баллов. Какая команда заняла третье место?
1) «Удар»
2) «Рывок»
3) «Взлёт»
4) «Спурт»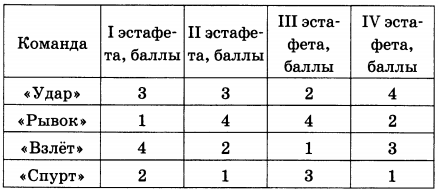
математика 8-9 класс
25239
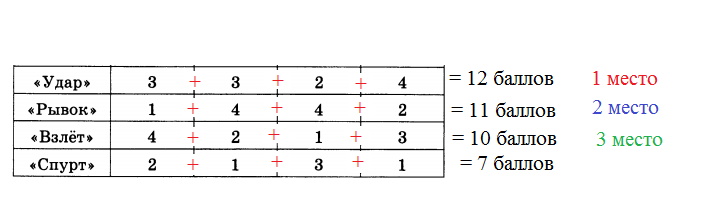
Решение
★
Все решения
