Задача 18237 Решите неравенство...

slava191

14.10.2017

Решите неравенство

1/(log3(2x-1)*log(x-1)9) < (log3sqrt(2x-1)) / (log3(x-1))

SOVA

14.10.2017

★

ОДЗ:
{2x-1 > 0 ⇒ x > 1/2
{x-1 > 0 и х-1 ≠ 1 ⇒ x > 1 и х ≠ 2
{ log_(3)(2x-1) ≠ 0 ⇒ 2x-1≠ 1 ⇒ x≠ 1
{log_(3)(x-1) ≠ 0 ⇒ x-1≠ 1 ⇒ x≠ 2
{log_(x-1)9 ≠ 0 ⇒ x≠ 2

ОДЗ: х ∈ (1;2)U(2;+ бесконечность)

Так как по формуле перехода к другому основанию:
log_(x-1)9=log_(3)9/log_(3)(x-1)=2/log_(3)(x-1)
и по формуле логарифма степени:
log_(3)sqrt(2x-1)=log_(3) (2x-1)^(1/2)=(1/2)log_(3)(2x-1)

Неравенство принимает вид:

(log_(3)(x-1))/(log_(3)(2x-1) - (log_(3)(2x-1))/(log_(3)(x-1)) < 0

или

(log^2_(3)(x-1)-log^2_(3)(2x-1))/ (log_(3)(2x-1)*log_(3)(x-1)) < 0

или

(log_(3)(x-1)-log_(3)(2x-1))(log_(3)(x-1)+log_(3)(2x-1))/ (log_(3)(2x-1)*log_(3)(x-1)) < 0

(log_(3)((x-1)/(2x-1))*log_(3)(x-1)(2x-1)/ (log_(3)(2x-1)*log_(3)(x-1)) < 0

Применяем обобщенный метод интервалов:
находим нули числителя.
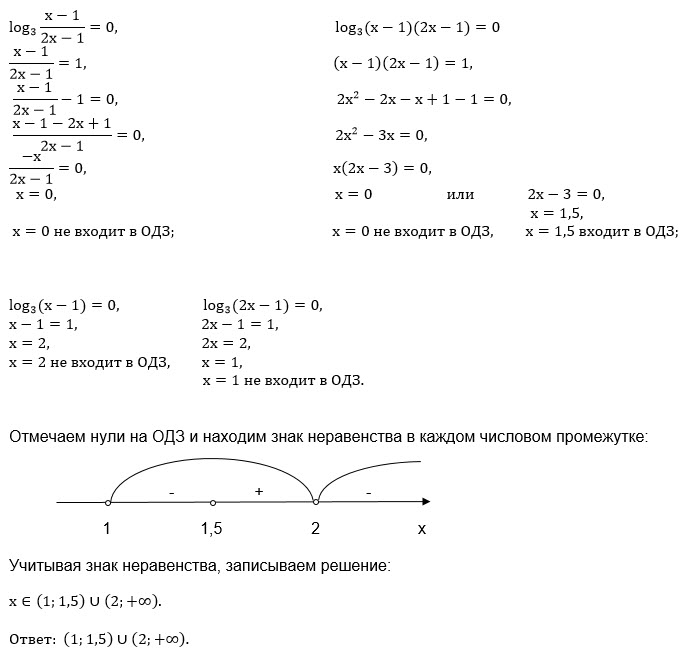
log_(3)((x-1)/(2x-1))=0 или log_(3)(x-1)(2x-1)=0

(x-1)/(2x-1)=1 или (х-1)(2х-1)=1

х-1=2х-1 или 2x^2-2x-х+1=1

x=0 или х*(2х - 3) =0 ⇒ х=0 или х=1,5

Нули знаменателя:
log_(3)(2x-1)=0 или log_(3)(x-1) = 0
х=1 или х=2

Отмечаем эти точки на ОДЗ
и расставляем знаки

(1) _-_(1,5) _+_ (2) ____-____

Выбираем точку например х=10 и находим знак каждого множителя и в числителе и в знаменателе.
Получаем знак -

О т в е т. (1; 1,5)U (2;+ бесконечность)