Задача 18230 Прямая y=-4x-11 является касательной к...
Условие
Решение
f`(x_(o))=k ( касательной)
Если прямые у=k_(1)x+b_(1) и у=k_(2)x+b_(2) параллельны, то k_(1)=k_(2)
У прямой у=-4х - 11
k=-4
значит k ( касательной)=-4
Находим
f`(x)=3x^2+14x+7
f`(x_(o))=3x^2_(o)+14x_(o)+7
3x^2_(o)+14x_(o)+7 = - 4
3x^2_(o)+14x_(o)+11 = 0
D=14^2-4*3*11=196-132=64=8^2
x_(o)=(-14-8)/6=-11/3 или х_(o)=(-14+8)/6= - 1
x_(o)=-11/3
при этом ордината прямой y=4x-11
y_(o)_(прямой)=-4*(-11/3)-11=11/3
ордината кривой y=x^3+7x^2+7x-6
y_(o)_(кривой)=(-11/3)^3+7*(-11/3)^2+7*(-11/3)-6=455/27
Точка с абсциссой (-11/3) не является точкой касания
х_(o)= - 1
ордината прямой y=4x-11
y_(o)_(прямой)=-4*(-1)-11=-7
ордината кривой y=x^3+7x^2+7x-6
y_(o)_(кривой)=(-1)^3+7*(-1)^2+7*(-1)-6=-7
О т в е т. -1
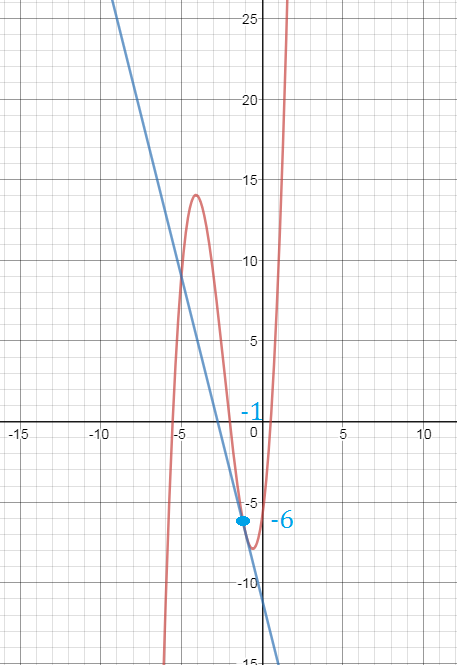
Все решения
(x 1)(x^2 6x 5)=(x 1)(x 1)(x 5)=0. Cледовательно ,х=-1 является корнем кратности два,а x=-5-корнем первой кратности . Поэтому точка А(-1;-7) -точка касания,а В(-5;9)-точка пересечения прямой y=-4x-11 и графика функции y=x^3 7x^2 7x-6. Ответ: -1.
