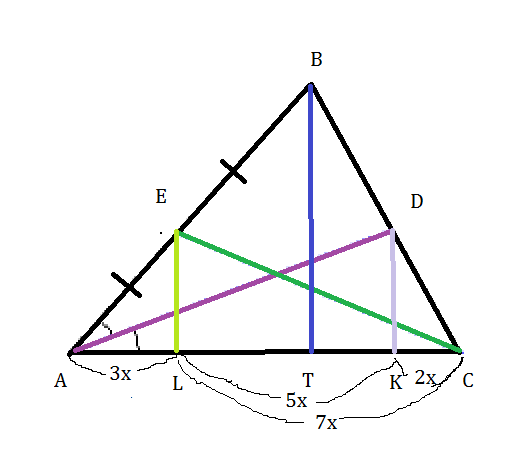
Задача 17984 В остроугольном треугольнике ABC...

slava191

07.10.2017

В остроугольном треугольнике ABC проведены биссектрисы AD и медиана CE, а точки K и L являются проекциями на сторону AC точек D и E соответственно, причем AK=4KC, AL=(3/7)LC.

а) Докажите, что AB=AC.

б) Найдите отношение AD:CE.

SOVA

07.10.2017

★

Пусть
АL=3х;LС=7х ( тогда АL=(3/7)LC)
КС=у, тогда АК=4у
LK=AK-AL=4у-3х, c другой стороны LK=LC-KC=7х-у
Приравниваем
4у-3х=7х-у ⇒ 5у=10х ⇒ у=2х


Итак,
АL=3х;LС=7х
КС=у=2х, тогда АК=4у=4*2х=8х

Тогда LT=5x.
Проведем высоту ВТ.
ВТ || EL
EL- средняя линия Δ АВТ.
AL=LT=3x
TK=KC=2x
DK- средняя линия Δ ВТС
и точка D - середина ВС
Значит AD и биссектриса и медиана Δ АВС ⇒
Δ АВС - равнобедренный,
АВ=АС
АС=10х, значит и АВ=10х

По теореме Пифагора из треугольника AEL
EL^2=AE^2-AL^2=(5x)^2-(3x)^2=16x^2
EL=4x

По теореме Пифагора из треугольника ELC
EC^2=EL^2+LC^2=16x^2+(7x)^2=65x^2
EC=xsqrt(65)

EL=DK=4x
По теореме Пифагора из треугольника АDK
AD^2=AK^2+DK^2
AD^2=(8x)^2+(4x)^2=80x^2
AD=xsqrt(80)

AD:CE=xsqrt(80):xsqrt(65)=sqrt(80)/sqrt(65)=sqrt(80/65)=
=sqrt(16/13)=4/sqrt(13)
О т в е т. 4:sqrt(13)