Задача 17944 а) Решите уравнение sinx=cos(Pi/3-x) б)...
Условие
б) Найдите корни на отрезке [4Pi; 16Pi/3]
математика 10-11 класс
17104
Решение
★
По формулам приведения
sinx=cos((Pi/2)-x)
Уравнение принимает вид
cos((Pi/2)-x)=cos((Pi/3)-x)
или
cos((Pi/2)-x)-cos((Pi/3)-x)=0
Применяем формулу
cos альфа - cos бета =-2sin(( альфа + бета )/2)*sin(( альфа - бета )/2)
-2sin((5Pi/12)-x)*sin(Pi/12) =0
⇒
sin((5Pi/12)-x)=0
пользуясь нечетностью синуса
уравнение можно записать так:
- sin(x-(5Pi/12))=0
x - (5Pi/12)=Pik, k ∈ Z
x=(5Pi/12)+Pik, k ∈ Z
О т в е т.
а) x=(5Pi/12)+Pik, k ∈ Z
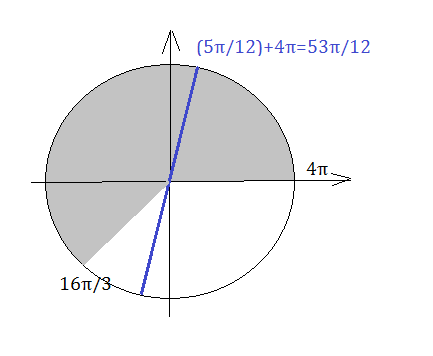
б) Указанному промежутку принадлежит один корень
х=(5Pi/12)+4Pi=53Pi/12
4Pi=48Pi/12 < 53Pi/12 < 64Pi/12=16Pi/3
Cм. рисунок