Задача 17868 ФИЗТЕХ МАТ-8) Найдите наибольшее...
Условие
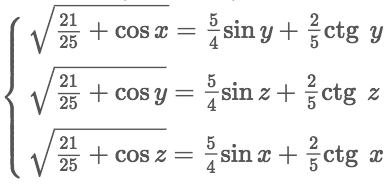
Решение
63/25=25/16(sin2x+sin2y+sin2z)+4/25(ctg2x+ctg2y+ctg2z)
Используем формулу ctg2a=1/sin2a–1
Получаем. 63/25=25/16(sin2x+sin2y+sin2z)+4/25(1/sin2x+1/sin2y+1/sin2z–3)
3=25/16(sin2x+sin2y+sin2z)+4/25(1/sin2x+1/sin2y+1/sin2z)
Далее, к правой части применим неравенство Коши.
a+b > =2√ab причем равенство достигается, если a=b.
.
Правая часть (ПЧ)
ПЧ > =2√25/16·sin2x·4/(25sin2x)+2√25/16·sin2y·4/(25sin2y)+2√25/16·sin2z·4/(25sin2z)
В каждой скобки синусы сократятся останется
ПЧ > =2(1/4)1/2+2(1/4)1/2+2(1/4)1/2=3
таким образом, у нас должно достигаться равенство, то есть 25/16sin2x=4/(25sin2x)== > sin4x=64/625 == > sin2x=8/25
аналогично sin2y=sin2z=8/25
cos(x+y+z)=cos(x) cos(y) cos(z) – cos(z) sin(x) sin(y) – cos(y) sin(x) sin(z) – cos(x) sin(y) sin(z)
Знаю sin2a мы можем восстановить другие тригонометрические функции с точностью до знака и подставить в верхнее выражение.
Далее несложно получить ответ –0.230894 (это тире, а не минус. Ответ совпал с поступашками)
Все решения

