Задача 17744 Cos2x+cos^2(x-p/2)=0,75 [P;5p/2]...
Условие
[P;5p/2]
предмет не задан
14467
Решение
★
По формулам приведения
cos((Pi/2)-x) = sinx
cos2x=1-2sin^2x
1-2sin^2x+(sinx)^2=3/4
sin^2x=1/4
sinx=1/2 или sinx=-1/2
sinx=1/2
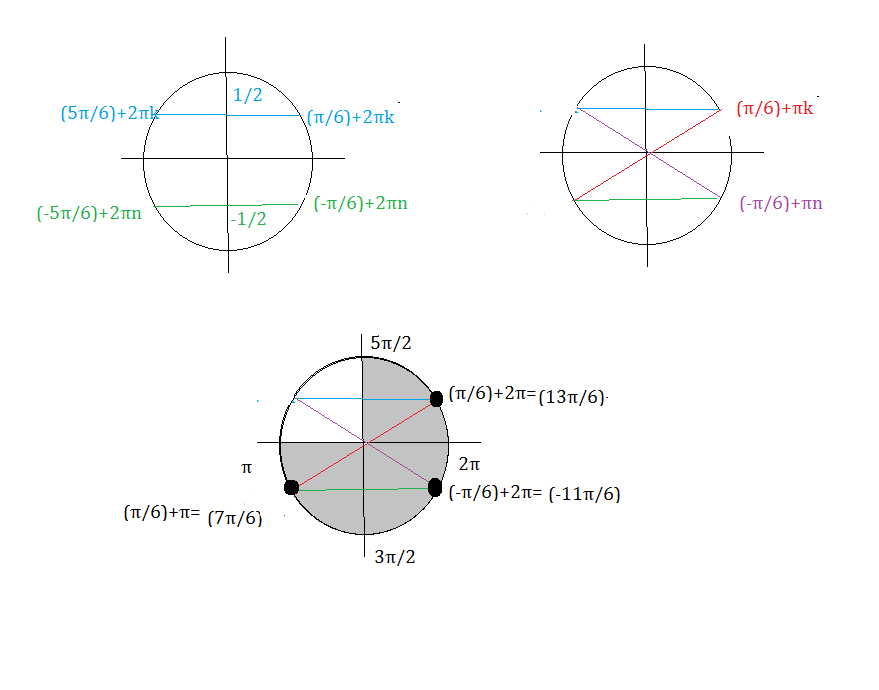
x= (π/6)+2πk или х=(5π/6)+2πk, k∈Z
sinx=-1/2
x= (-π/6)+2πn или х=(-5π/6)+2πn, n∈Z
Эти четыре серии ответов можно записать так:
x= (π/6)+πk или х=(-π/6)+πn, k,n∈Z
Указанному промежутку принадлежат корни
х=(π/6)+π=(7π/6)
х=(-π/6)+2π=(11π/6)
х=(π/6)+2π=(13π/6)
О т в е т.
а)(π/6)+πk; (-π/6)+πn; k,n∈Z
б) (7π/6);(11π/6);(13π/6) - корни, принадлежащие отрезку
[Pi;5Pi/2]