Задача 17666 Решите неравенство корень 5ой степени из...
Условие
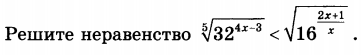
математика 10-11 класс
26321
Решение
★
4x-3-(4x+2)/x < 0, (4x^2-7x-2)/x < 0, 4(x-2)(x+1/4)/x < 0, решаем методом интервалов и получаем, что x ∈(- бесконечность;-1/4) ∪ (0;2)
Все решения
