Задача 17640 а) Решите уравнение (x+3)^2/5 +...
Условие
б) Найдите его корни, принадлежащие отрезку [-6; -4]
математика 10-11 класс
55241
Решение
★
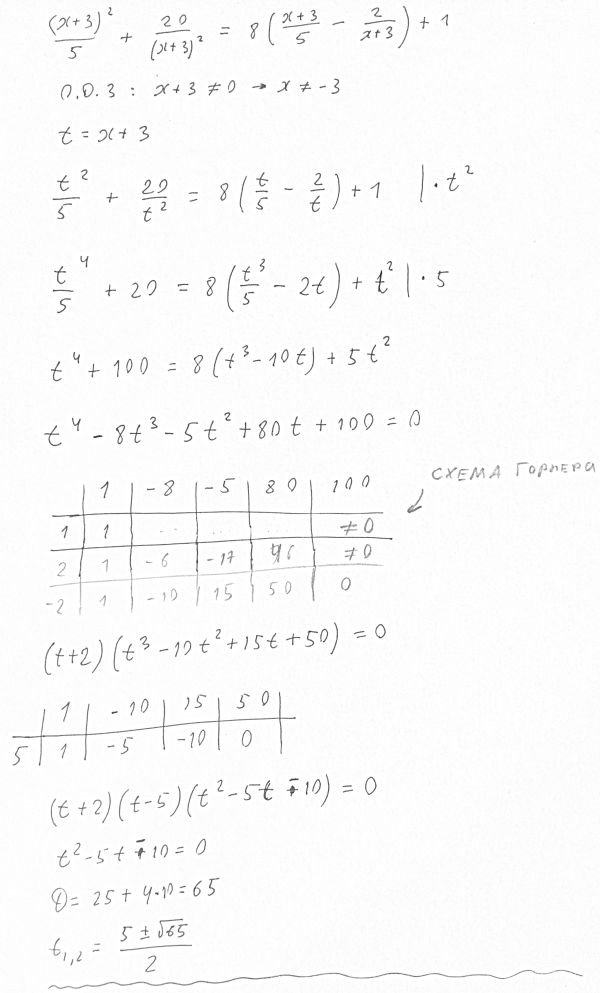
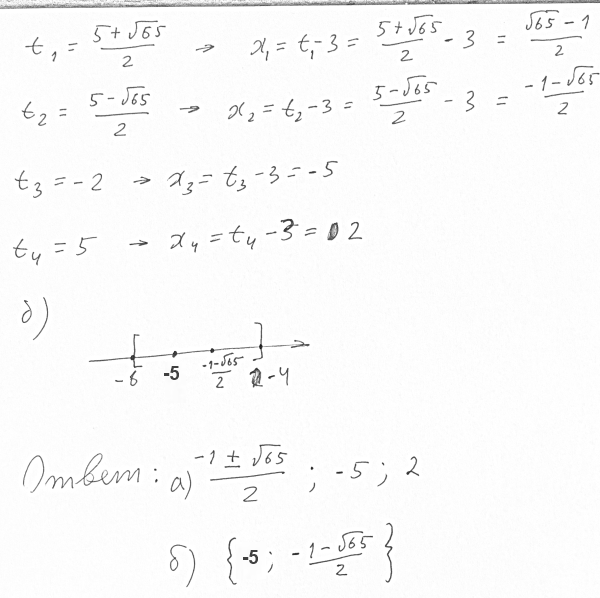
Все решения
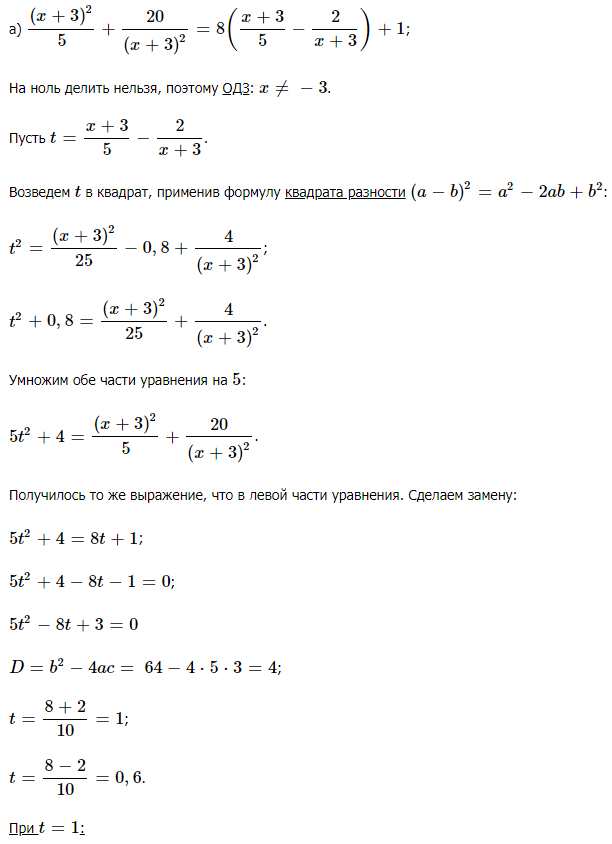
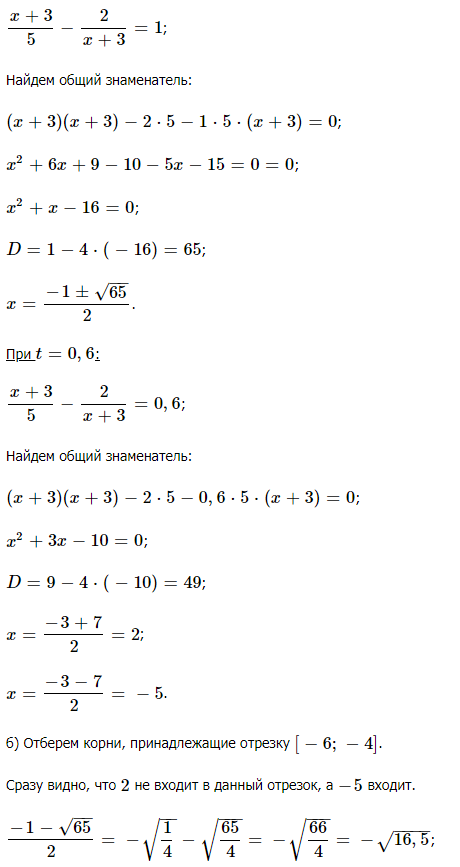
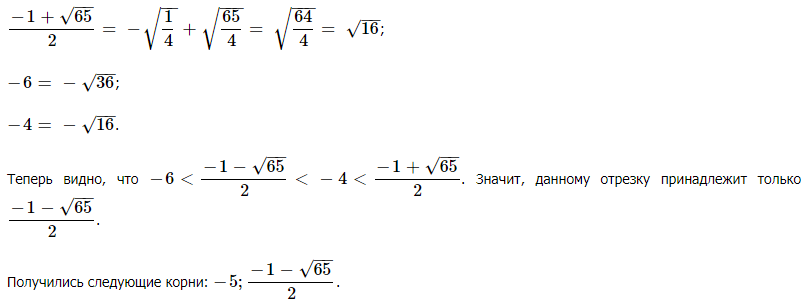
тогда получим у^2/5+20/(y^2)=8(y/5-2/y)+1
приведем все к общему знаменателю 5Y^2 и рассмотрим числители после этого
y^4+100=8(y^3-10y)+5y^2
y^4-8y^3-5y^2+80y+100=0
(y+2)(y-5)(y^2-5y-10)=0
D=25+40=65
y1=-2; y2=5; y3=(5+корень из 65)/2; y4=5+корень из 65)/2
соответственно
x1= -5; x2=2; x3= 0.5 ( корня из 65)-0.5; x4= -0.5 корня из 65-0.5
