Задача 17558 Основания равнобедренной трапеции равны...

slava191

19.09.2017

Основания равнобедренной трапеции равны 120 и 50. Центр окружности, описанной около трапеции, лежит внутри трапеции, а радиус окружности равен 65. Найдите высоту трапеции.

vk318474530

24.09.2017

★

Высота трапеции в данном случае есть ничто иное, как сумма высот двух равнобедренных треугольников AOB и DOC, опущенных на их основания AB и DC соответственно.

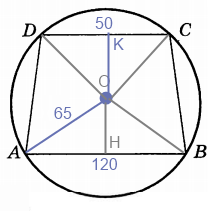
OA = OB = DO = OC = r = 65.
AH = AB/2 = 120/2 = 60.

[b]Перейдем к вычислениям.[/b]

Высота треугольника AOB вычисляется по теореме Пифагора:

OH = sqrt(AO^2-AH^2) = sqrt(65^2-60^2) = 25

Аналогично для высоты треугольника DOC

OK = sqrt(65^2-25^2) = 60

Следовательно высота трапеции равно KH = OH + OK = 25+60 = 85.

[b]Ответ:[/b] 85