Задача 17505 Найдите точку минимума функции...

slava191

17.09.2017

Найдите точку минимума функции y=(10-x)e^(10-x)

vk318474530

18.09.2017

★

Найдем производную функции.

y' = (10-x)'e^(10-x) + (10-x)(e^(10-x))' = -e^(10-x) + (10-x)(-e^(10-x)) = -e^(10-x)(1+10-x) = -e^(10-x)(11-x)

Приравняем производную к нулю и найдем экстремумы функции.

-e^(10-x)(11-x) = 0

(x-11)*e^(10-x) = 0

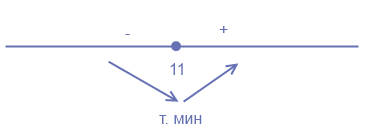
x = 11

Отобразим знаки производной функции на графике, который наглядно показывает, что точка x=11 является точкой минимума данной функции.

[b]Ответ:[/b] 11