Задача 17168 а) Решите уравнение...
Условие
б) Найти корни.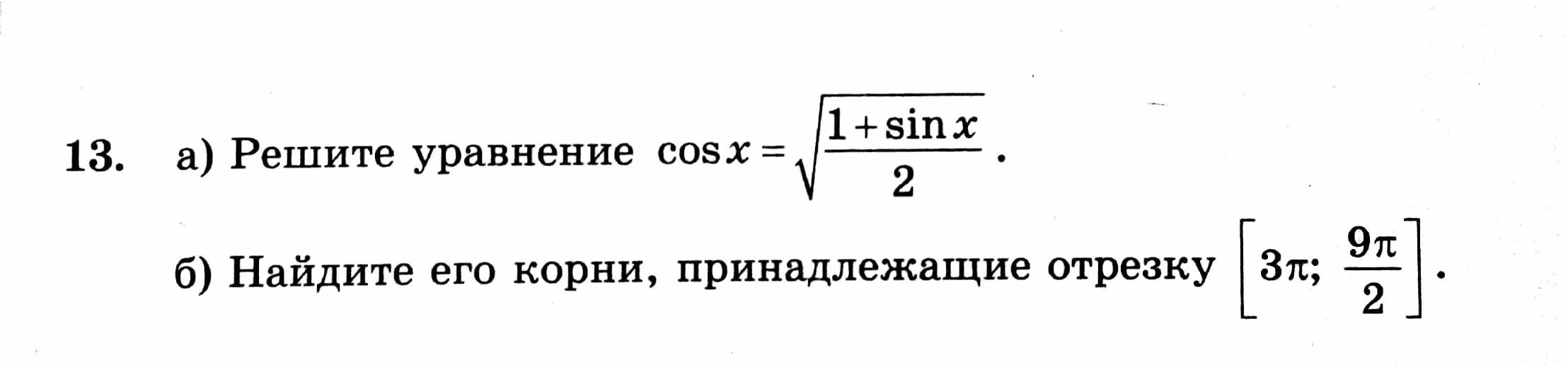
Решение
{(1+sinx)/2 больше или равно 0 ⇒ 1+sinx больше или равно 0
{cosx больше или равно 0
⇒
{ sinx больше или равно - 1
{(-Pi/2)+2Pi*t меньше или равно х меньше или равно (Pi/2)+2Pi*t, t∈Z.
{х ∈ (- бесконечность ;+ бесконечность )
{(-Pi/2)+2Pi*t меньше или равно х меньше или равно (Pi/2)+2Pi*t, t∈Z.
x ∈ [(-Pi/2)+2Pi*n; (Pi/2)+2Pi*n], n∈Z.
Возводим обе части уравнения в квадрат.
сos^2x=(1+sinx)/2
2cos^2x=1+sinx
2-2sin^2x=1+sinx
2sin^2x+sinx-1=0
D=1+8=9
sinx=-1 или sinx=1/2
x=-Pi/2+2Pi*k или х=(Pi/6)+2Pi*m или х=(5Pi/6)+2Pi*n, k,m,n ∈ Z.
С учетом ОДЗ получаем ответ
О т в е т.
а)( -Pi/2)+2Pi*k ;(Pi/6)+2Pi*m k,m ∈ Z.
б) Указанному промежутку принадлежат корни
( -Pi/2)+4Pi=7Pi/2
и
(Pi/6)+4Pi=25Pi/6