Задача 16905 Решите систему уравнений...
Условие
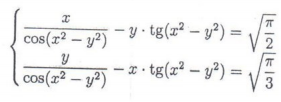
Решение
cos(x^2-y^2) ≠ 0
Систему запишем в виде:
{х-ysin(x^2-y^2)=sqrt(Pi/2)cos(x^2-y^2);
{y-xsin(x^2-y^2)=sqrt(Pi/3)cos(x^2-y^2).
Сложим уравнения и вычтем из первого второе:
{(x+y)-(x+y)sin(x^2-y^2)=(sqrt(Pi/2)+sqrt(Pi/3))*cos(x^2-y^2);
{(x-y)+(x-y)sin(x^2-y^2)=(sqrt(Pi/2)-sqrt(Pi/3))*cos(x^2-y^2).
Разложим левую часть каждого уравнения на множители, получим систему (#):
{(x+y)*(1-sin(x^2-y^2))=(sqrt(Pi/2)+sqrt(Pi/3))*cos(x^2-y^2);
{(x-y)*(1+sin(x^2-y^2))=(sqrt(Pi/2)-sqrt(Pi/3))*cos(x^2-y^2).
Перемножим уравнения
(x^2-y^2)*(1-sin^2(x^2-y^2))=((sqrt(Pi/2))^2-sqrt(Pi/3))^2)*cos^2(x^2-y^2).
(x^2-y^2)*cos^2(x^2-y^2)=(Pi/6)cos^2(x^2-y^2)
Переносим все слагаемые влево и раскладываем на множители:
(x^2-y^2-(Pi/6))*cos^2(x^2-y^2)=0
Так как
сos(x^2-y^2)=0 не удовлетворяет ОДЗ системы, то
cos^2(x^2-y^2) ≠0, и значит
x^2-y^2= Pi/6
Подставляем это значение в систему (#)
{(x+y)*(1-sin(Pi/6))=(sqrt(Pi/2)+sqrt(Pi/3))*cos(Pi/6);
{(x-y)*(1+sin(Pi/6))=(sqrt(Pi/2)-sqrt(Pi/3))*cos(Pi/6).
{x+y=sqrt(3)*sqrt(Pi)*(sqrt(3)+sqrt(2))/sqrt(6);
{x-y=(sqrt(3)/3)*sqrt(Pi)*(sqrt(3)-sqrt(2))/sqrt(6).
Cкладываем два уравнения и находим х
х=((2sqrt(3)+sqrt(2))*sqrt(Pi))/(3sqrt(2)).
Вычитаем из первого второе и находим у
у=((sqrt(3)+2sqrt(2))*sqrt(Pi))/(3sqrt(2)).
О т в е т.( ((2sqrt(3)+sqrt(2))*sqrt(Pi))/(3sqrt(2));((sqrt(3)+2sqrt(2))*sqrt(Pi))/(3sqrt(2))).