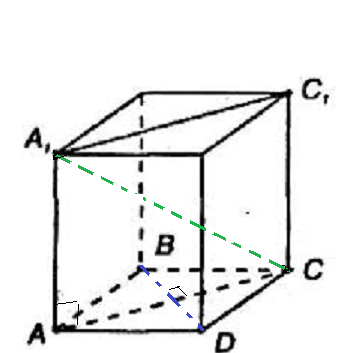
Задача 16862 Основанием прямой четырехугольной призмы...

slava191

17.07.2017

Основанием прямой четырехугольной призмы ABCDA1B1C1D1 является ромб ABCD, AB=AA1

а) Докажите, что прямые А1С и BD перпендикулярны

б) Найдите объем призмы, если А1С=BD=2.

SOVA

17.07.2017

★

а)Диагонали ромба взаимно перпендикулярны, значит
АС ⊥ BD.

Призма прямая , боковые ребра перпендикулярны плоскости основания
А1А ⊥ АС

По теореме о трех перпендикулярах, АС - проекция А1С
и АС перпендикулярна BD, значит и наклонная А1С перпендикулярна BD.

б) Пусть АВ=ВС=СD=AD=x
По условию
АВ=АА1 и значит АА1=х
Применяем формулу, связывающую квадраты диагоналей параллелограмма и его стороны:
d^2_(1)+d^2_(2)=2*(a^2+b^2)

AC^2+BD^2=4x^2
AC^2+2^2=4x^2
AC^2=4x^2-4

По теореме Пифагора из прямоугольного треугольника АА1С:
А1С^2=A1A^2+AC^2
2^2=x^2+(4x^2-4)
5x^2=8
x^2=8/5
x=sqrt(8/5)

V(призмы)=S(ромба)*H=(1/2)d_(1)*d_(2)*AA1=
=(1/2)2*sqrt(4x^2-4)*x=
=(1/2)*2*sqrt(4*(8/5)-4)*sqrt(8/5)= sqrt(12/5)*sqrt(8/5)=4sqrt(6)/5

О т в е т. 4sqrt(6)/5