Задача 16860 а) Решите уравнение...
Условие
б) Укажите корни этого уравнения, принадлежащие отрезку [-Pi/2; Pi]
математика 10-11 класс
81895
Решение
★
Разложим левую часть уравнения на множители способом группировки
(2xcosx–8cosx)+(x–4)=0;
2cosx*(x-4)+(x-4)=0;
(x-4)*(2cosx+1)=0
Произведение двух множителей равно 0 тогда и только тогда когда хотя бы один из множителей равен 0, а другой при этом не теряет смысла.
x-4=0 или 2cosx+1=0
x=4 или сosx=-1/2 ⇒ ± (2π/3)+2πk, k∈Z
О т в е т.
а) 4; ± (2π/3)+2πk, k∈Z
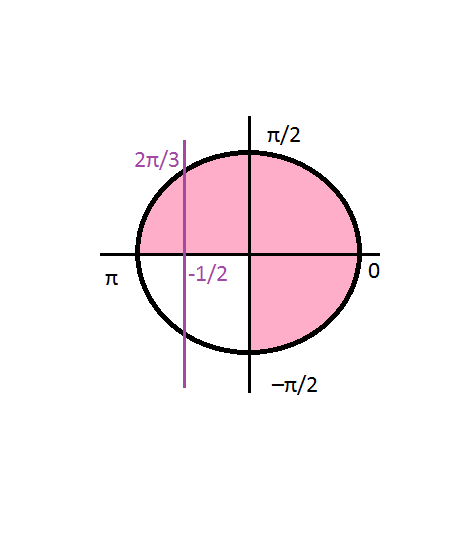
б) (2π/3)∈ [–π/2; π] cм. рисунок.