Задача 16808 ...

slava191

11.07.2017

а) Решите уравнение 4sin^2x=-4sin(-x)-1.

б) Найдите все корни этого уравнения, принадлежащие промежутку [-2π;-π/2].

Geniys

11.07.2017

★

а)
4sin^(2)x+4sin(–x)+1=0
sin(–x)= - sin (x)
4sin^(2)x-4sin(x)+1=0
Пусть t= sin x, t ∈ [-1,1].
4t^(2)-4t+1=0
D=16-4*4*1=0 - один корень
x=4/(2*4)=0,5
Обратная замена
sin x=0,5
x=Pi/6 + 2 Pi n, n ∈ Z,
x=5Pi/6 + 2 Pi n;

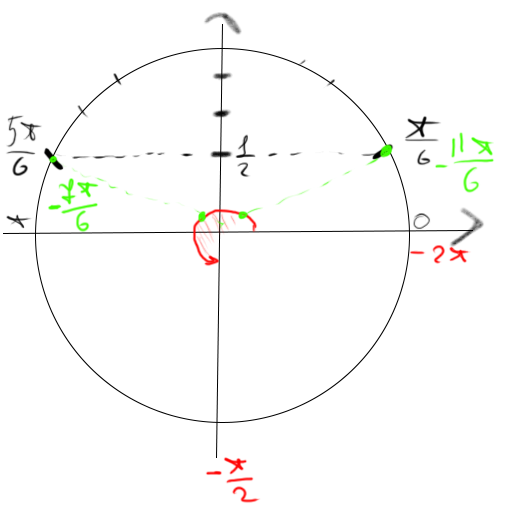
б) (см рисунок)

Ответ:
a)x=Pi/6 + 2 Pi n, n ∈ Z,
x=5Pi/6 + 2 Pi n;
б)-11Pi/6 и -7Pi/6