Задача 16786 Решите неравенство (9^x+5*3^x-14) /...
Условие
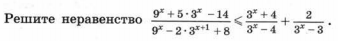
Решение
3^x=t;
t > 0.
3^(x+1)=3^x*3=3t;
9^x=(3^2)^x=(3^x)^2=t^2.
Неравенство принимает вид:
(t^2+5t-14)/(t^2-6t+8) меньше или равно ((t+4)/(t-4)) + (2/(t-3));
переносим все слагаемые влево и приводим дроби к общему знаменателю:
t^2-6t+8=(t-4)(t-2)
((t-3)*(t^2+5t-14)-(t+4)*(t-2)(t-3)-2*(t-4)(t-2))/(t-2)(t-3)(t-4) меньше или равно 0;
(t^2-3t+2)/(t-2)(t-3)(t-4) меньше или равно 0;
(t-1)(t-2)/(t-2)(t-3)(t-4) меньше или равно 0.
Применяем метод интервалов.
_-__[1] _+__ (2) __+__ (3) __-__ (4) __+__
t меньше или равно 1 или 3 < t < 4
Возвращаемся к переменной х:
3^x меньше или равно 1 или 3 < 3^x < 4
x меньше или равно 0 или 1 < x < log_(3)4
О т в е т. (- бесконечность;0]U(1;log_(3)4)