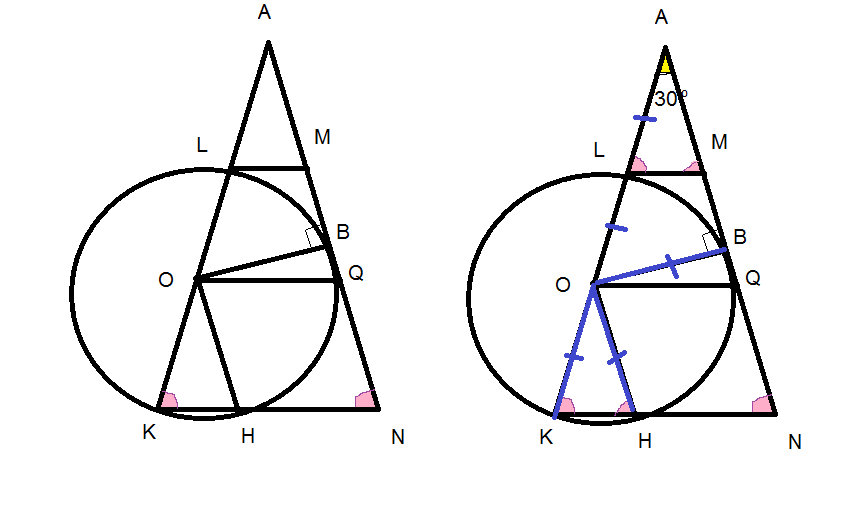Задача 16760 Дана равнобедренная трапеция KLMN с...

slava191

30.06.2017

Дана равнобедренная трапеция KLMN с основаниями KN и LM. Окружность с центром О, построенная на боковой стороне KL как на диаметре, касается боковой стороны MN и второй раз пересекает большее основание KN в точке Н, точка Q — середина MN.

а) Докажите, что четырёхугольник NQOH — параллелограмм.

б) Найдите KN, если угол LKN = 75° и LM = 4.

SOVA

04.07.2017

★

Дано:
LM||KN;
KL=MN.

OK=OL=r

OH=r
OB=r
OB⊥MN

а)

OQ-средняя линия трапеции KLMN
OQ||LM
OQ||KN ⇒ OQ||HN
OK=OL=OH=OB=r
Δ KOH- равнобедренный (ОК=ОН=r)
∠ OKH=∠OHK=75 градусов;

∠OHK=∠QNK=75 градусов, это односторонние углы, значит
OH||QN
NQOH- параллелограмм, так как противоположные стороны попарно параллельны:
OQ||HN
и
OH||QN

б)
Дано:
∠ LKN=∠MNK=75 градусов;
LM=4

Пусть боковые стороны трапеции LK и MN пересекаются в точке А.
∠ АLМ=∠ LKN=75 градусов;
∠АML=∠MNK=75 градусов;
Значит, ∠ АLМ=∠АML=75 градусов;
Δ ALM - равнобедренный
∠ LAM=180 градусов - ∠ АLМ-∠АML=180 градусов -75 градусов-75 градусов=30 градусов;

ΔАОВ- прямоугольный (OB⊥MN) с острым углом ∠ LAM=30 градусов, катет против угла в 30 градусов равен половине гипотенузы
ОА=2*ОВ=2*r

Тогда AL=AO-LO=2r-r=r
AL=AM=r
LM- средняя линия треугольника AOQ
OQ=2LM=2*4=8

ΔАLM=ΔKOH
AL=AM=OK=OH=r
LM=KH=4

KN=KH+HN=LM+OQ=4+8=12
О т в е т. 12