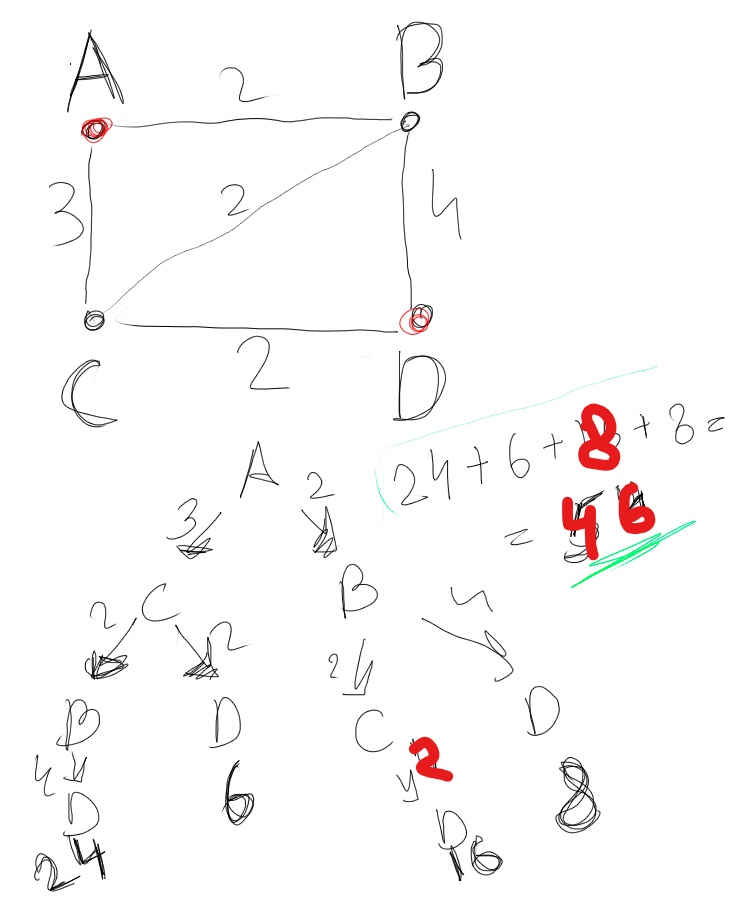
Задача 16411 15) На карту нанесены 4 города (А, В, С...
Условие
Известно, что:
между городами А и С — три дороги,
между городами С и В — две дороги,
между городами А и В — две дороги,
между городами С и D — две дороги,
между городами В и D — четыре дороги.
По каждой из этих дорог можно ехать в обе стороны. Сколькими различными способами можно проехать из А в D, посещая каждый город не более одного раза?
информатика 10-11 класс
6767
Решение
★
2) построим дерево игры
(см рисунок)
Ответ 46