Задача 164 На рисунке показана стоимость одной...
Условие
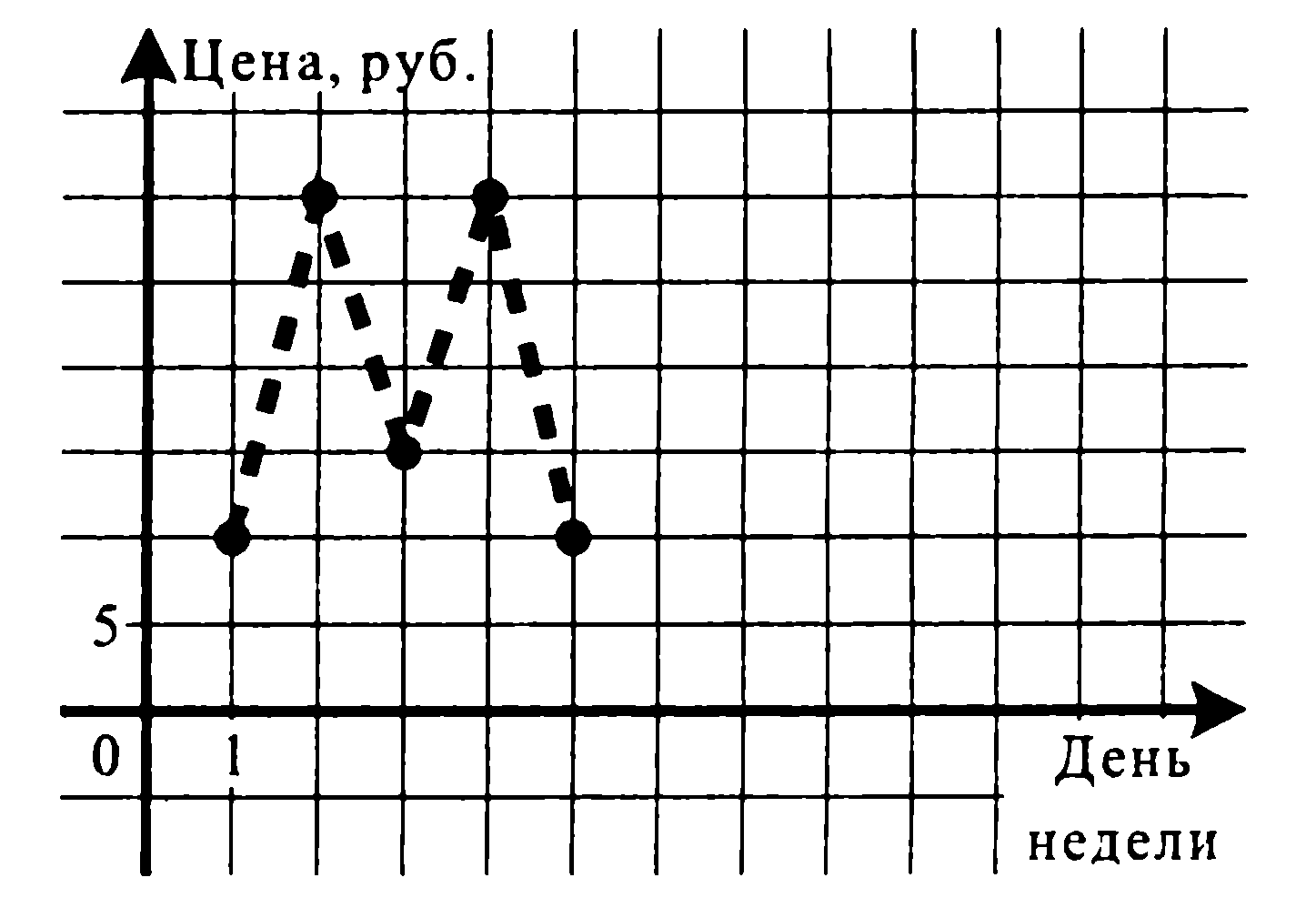
Решение
биржевых торгах. Но в этой условной ситуации мы используем все
возможности «купить подешевле — продать подороже». В первый
день на 500 рублей покупаем 50 акций по 10 рублей. Во второй день
продаем их по 30 рублей за штуку. В третий день на полученные
1500 рублей мы покупаем 100 акций по 15 рублей. Заключительная
сделка произойдет в четвертый день, 100 акций будут проданы по
30 рублей. Вычитая из полученных в итоге 3000 рублей те 500
рублей, которые были вначале, вычисляем доход — 2500 рублей.
Ответ: 2500