Задача 16379 Дан фрагмент электронной таблицы....
Условие
Какое целое число должно быть записано в ячейке A1, чтобы диаграмма, построенная по значениям ячеек диапазона A2:С2, соответствовала рисунку? Известно, что все значения ячеек из рассматриваемого диапазона неотрицательны.
КИМ ЕГЭ 2017 (досрочный период)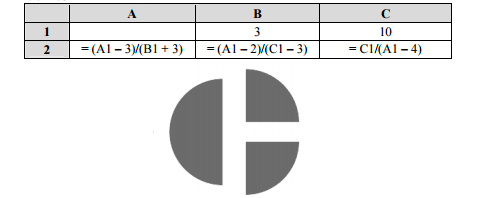
информатика 10-11 класс
10405
Решение
A2=(x-3)/6;
B2=(x-2)/7;
C2=10/(x-4);
На рисунке видно, что две ячейки равны.
(x-3)/6=(x-2)/7
x=9
Подставим и получим:
A2=1
B2=1
С2=2.
Число 9 подходит
Ответ: 9