Задача 16374 Логическая функция F задаётся выражением...
Условие
На рисунке приведён фрагмент таблицы истинности функции F, содержащий
все наборы аргументов, при которых функция F истинна.
Определите, какому столбцу таблицы истинности функции F соответствует
каждая из переменных w, x, y, z.
В ответе напишите буквы w, x, y, z в том порядке, в котором идут
соответствующие им столбцы (сначала – буква, соответствующая первому
столбцу; затем – буква, соответствующая второму столбцу, и т.д.) Буквы
в ответе пишите подряд, никаких разделителей между буквами ставить
не нужно.
Пример. Если бы функция была задана выражением ¬x \/ y, зависящим от
двух переменных: x и y, и был приведён фрагмент её таблицы истинности,
содержащий все наборы аргументов, при которых функция истинна.
Тогда первому столбцу соответствовала бы переменная y, а второму
столбцу – переменная x. В ответе следовало бы написать: yx.
КИМ ЕГЭ 2017 (досрочный период)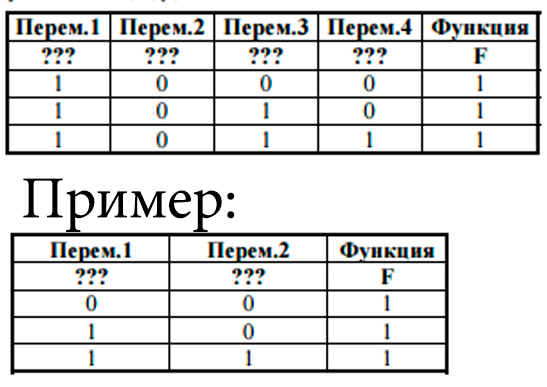
Решение
Для того чтобы вырождении было истинно в любой строчке должны выполнятся равенства x=1, ¬y=1, (¬z \/ w)=1. Отсюда следует, что x=1, y=0, поэтому x-первый столбик, y- второй столбик.
Разберём случае когда выполняется равенство (¬z \/ w)=1
1)z=0, w=1
2)z=0, w=0
3)z=1, w=1
Можно заметить, что z- это четвёртый столбик, а w-третий
Ответ: xywz