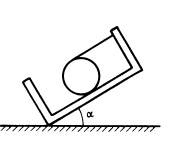
На плоском шероховатом дне чаши находится шар (рис). Дно чаши наклонено на некоторый угол по отношению к горизонту. Шар удерживается в равновесии нитью, параллельной дну. На какой наибольший угол а можно наклонить дно чаши, чтобы шар все еще оставался в равновесии? Коэффициент трения к = 0,5.
физика 10-11 класс
9692
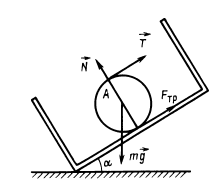
Силы, действующие на шар, изображены на рис. Сумма проекций сил на направление, перпендикулярное к дну чаши, должна быть равна нулю. Проекции на это направление имеют только сила тяжести mg и реакция дна чаши N. Таким образом, N=mgcosa. Следовательно, сила трения
Fтр<=kmgcosa. (1)
Запишем уравнение моментов относительно оси, проходящей через точку А перпендикулярно плоскости рисунка: 2RFTp — mgi?sina = 0, R — радиус шара, отсюда Fтp=mgsin a/2.
Учитывая неравенство (1) найдем, что при равновесии
kmgcosa>=mg sin a/2.
Следовательно, максимальный угол а определяется из условия tga=2k=l, a = 45°.
Ответ: 45°
Вопросы к решению (1)
mg*sina должно быть имелось ввиду

