Задача 16282 ...

Geniys

05.06.2017

На числовой прямой даны два отрезка: P = [20, 50] и Q = [30,65]. Отрезок A таков, что формула

¬(x ∈ A) → ((x ∈ P) →¬ (x ∈ Q))

истинна при любом значении переменной x.

Какова наименьшая возможная длина отрезка A?
(ФИПИ)

Заменим (x ∈ A)=А
( x ∈ P)=P
(x ∈ Q)=Q
Упростим
A+¬P+¬Q=1 *
Нарисуем рисунок и отметим интервалы.
Рассмотрим каждый из отрезков по отдельности
1) и 5) А+1+1=1 А-любое
2) A+0+1=1 А-любое
3) A+0+0=1 А=1 . Для выполнения равенства А обязательно должно находит на интервале [30;50]
4) A+1+0=1 А-любое

50-30=20

*a→b=¬a+b
*¬(¬a)=a




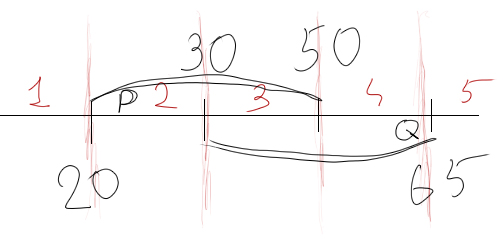
Ответ: 20