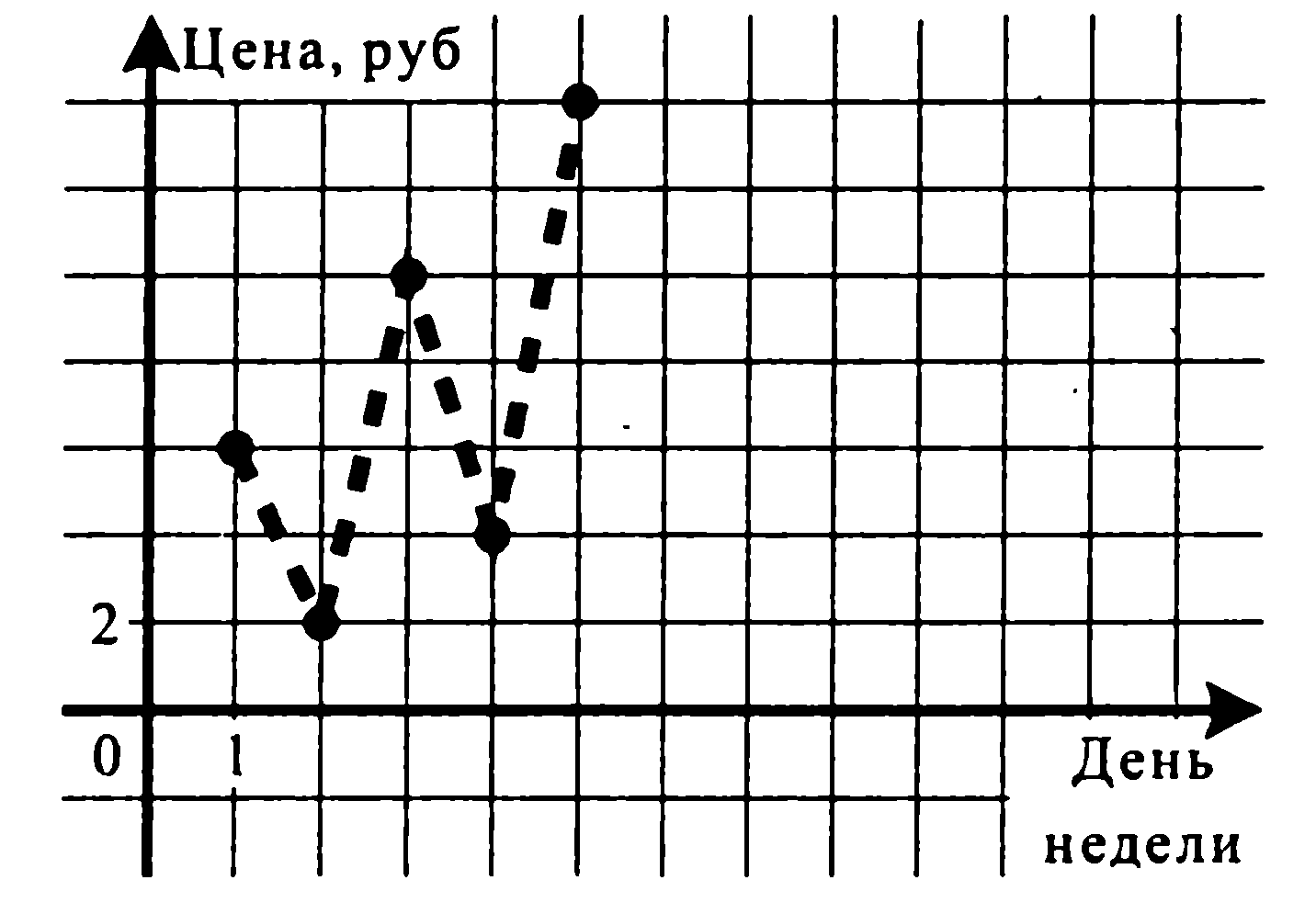
На рисунке показана стоимость одной акции предприятия в рублях в течение недели биржевых торгов. Определите доход в рублях, который можно получить, если на этой неделе купить и продать 80 акций.
математика 10-11 класс
5456
При выполнении этого задания надо обратить внимание на тот факт, что выгоднее всего купить акции во второй день по минимальной цене 2 рубля за акцию, а продать их в пятый день по максимальной цене 14 рублей за акцию. Умножив доход на каждой акции 12 рублей на 80, получим ответ.
Ответ: 960
Вопросы к решению (1)
почему мы умножаем 12 на 80, если выгоднее продавать по 14 рублей за 1 акцию. тогда получается 14 умножаем на 80 и получается 1120

