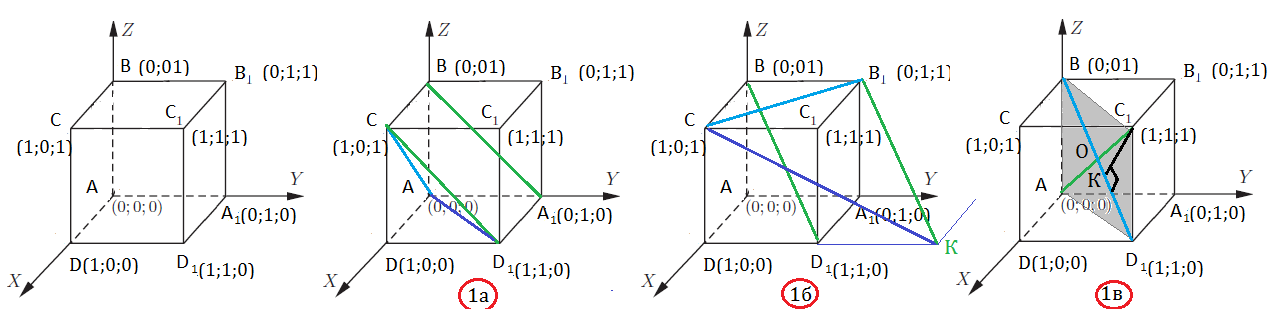
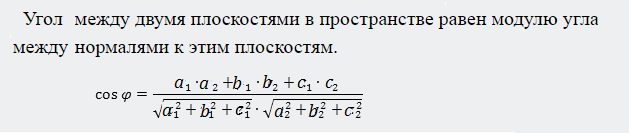Задача 16071 В системе координат Oxyz расположен куб...

slava191

28.05.2017

В системе координат Oxyz расположен куб АВСВА1В1С1В1 так, что D(1;0;0), C1(1;1;1), А1(0;1;0), А(0;0;0). Постройте этот куб. Векторно-координатным методом найдите:

1. Угол между прямыми:
а) А1В и АС;
б) D1В и В1С;
в) АС1 и D1В.

2. Синус угла между прямой и плоскостью:
а) ВС и (АВ1D1);
б) А1В и (АВ1С);
в) В1D1 и (АВ1С);
г) А1В и (ВС1D).

3. Угол между плоскостями:
а) АВ1С и АВС1;
б) АВ1С и А1ВС1;
в) D1АС и В1АС.

SOVA

30.05.2017

★

1 а)
Проводим D1C || A1В. Плоскость D1СA || A1В.
Cоставляем уравнение плоскости D1СA
Пусть M (х;у;z) - произвольная точка этой плоскости.
Векторы
vector{AM} (x;y;z); vector{AD1} (1;1;0) и vector{AC1}(1;0;1)
компланарны (лежат в одной плоскости).
Записываем условие компланарности векторов: определитель третьего порядка, составленный из координат этих векторов равен 0.
Раскрываем этот определитель и получаем уравнение плоскости D1CA
x-y-z=0
Расстояние от любой точки прямой А1В, например от точки В, и есть расстояние между прямыми.
d(B)=|(x_(в)-у_(в)-z_(в)|/sqrt(3)=|0-0-1|/sqrt(3)=1/sqrt(3).

1б)
Проводим B1K || BD1. Плоскость B1KC || BD1
Cоставляем уравнение плоскости B1KC
K(1;2;0)
Пусть M (х;у;z) - произвольная точка этой плоскости.
Векторы
vector{KM} (x;y;z); vector{B1K} (1;1;-1) и vector{CK}(0;2;-1)
компланарны (лежат в одной плоскости).
Записываем условие компланарности векторов: определитель третьего порядка, составленный из координат этих векторов равен 0.
Раскрываем этот определитель и получаем уравнение плоскости B1KC:
x+y+2z-3=0
Расстояние от любой точки прямой А1В, например от точки В, и есть расстояние между прямыми.
d(B)=|(x_(в)+у_(в)+2z_(в)-3|/sqrt(1+1+4)=|0+0+2*1-3|/sqrt(6)=1/sqrt(6).

1в)
Диагонали куба АС1 и D1B пересекаются в точке O- центре куба.
vector{AC1}(1;1;1)
vector{D1B}(-1;-1;1)
Их скалярное произведение
vector{AC1}*vector{D1B}=-1-1+1=-1
|vector{AC1}|=sqrt(3)
|vector{D1B}|=sqrt(3)
cos∠(vector{AC1},vector{D1B})=-1/3
sin∠(vector{AC1},vector{D1B})=sqrt(1-(-1/3)^2)=sqrt(8/9)=
=2sqrt(2)/3
d=|C1K|=|OC1|*sin∠(vector{AC1},vector{D1B})=
=(sqrt(3)/2)*(2sqrt(2))/(3)=sqrt(6)/3

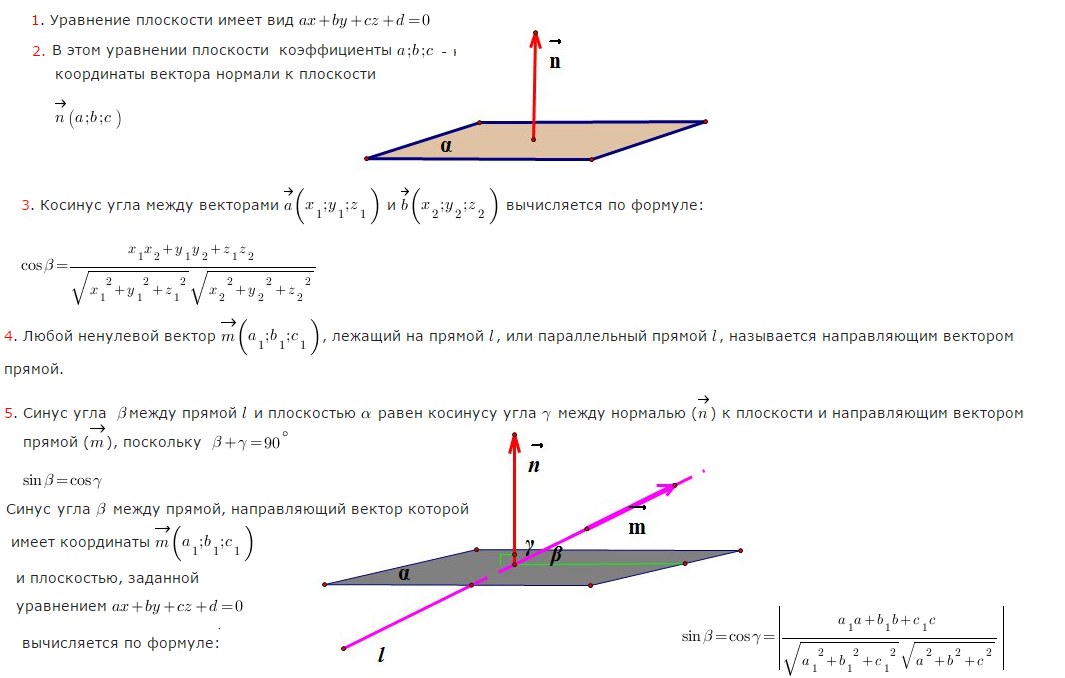
Cм. Теоретические сведения для решения задачи 2 в приложении 2.
2а)
Cоставляем уравнение плоскости AB1D1:
Пусть M (х;у;z) - произвольная точка этой плоскости.
Векторы
vector{AM} (x;y;z); vector{AB1} (0;1;1) и vector{AD1}(1;1;0)
компланарны (лежат в одной плоскости).
Записываем условие компланарности векторов: определитель третьего порядка, составленный из координат этих векторов равен 0.
Раскрываем этот определитель и получаем уравнение плоскости AB1D1:x-y+z=0
vector{n}(1;-1;1)
vector{m}= vector{BC}(1;0;0)
sin β=|1+0+0|/(1*sqrt(3))=1/sqrt(3)

2б)
Cоставляем уравнение плоскости AB1С:
Пусть M (х;у;z) - произвольная точка этой плоскости.
Векторы
vector{AM} (x;y;z); vector{AB1} (0;1;1) и vector{AС}(1;0;1)
компланарны (лежат в одной плоскости).
Записываем условие компланарности векторов: определитель третьего порядка, составленный из координат этих векторов равен 0.
Раскрываем этот определитель и получаем уравнение плоскости AB1С:
х+y-z=0
vector{n}(1;1;-1)
vector{m}= vector{А1B}(0;-1;1)
sin β=|0-1-1|/(sqrt(2)*sqrt(3))=2/(sqrt(2)*sqrt(3))=sqrt(2/3)

2в)
Cоставляем уравнение плоскости AB1С ( см. п.2б))
х+y-z=0
vector{n}(1;1;-1)
vector{m}= vector{B1D1}(1;0;-1)
sin β=|1+0+1|/(sqrt(2)*sqrt(3))=2/(sqrt(2)*sqrt(3))=sqrt(2/3)

2г)
Cоставляем уравнение плоскости BC1D:
Пусть M (х;у;z) - произвольная точка этой плоскости.
Векторы
vector{BM} (x;y;z-1); vector{BC1} (1;1;0) и vector{BD}(1;0;-1)
компланарны (лежат в одной плоскости).
Записываем условие компланарности векторов: определитель третьего порядка, составленный из координат этих векторов равен 0.
Раскрываем этот определитель и получаем уравнение плоскости BC1D::
x-y+z-1=0
vector{n}(1;1;-1)
vector{m}= vector{А1B}(0;-1;1)
sin β=|0+1+1|/(sqrt(2)*sqrt(3))=2/(sqrt(2)*sqrt(3))=sqrt(2/3)

Cм. Теоретические сведения для решения задачи 3 в приложении 3.
3а)
Cоставляем уравнение плоскости AB1C ( cм. пункт 2б) :
х+y-z=0
vector{n1}(1;1;-1)
Cоставляем уравнение плоскости ABС1:
Пусть M (х;у;z) - произвольная точка этой плоскости.
Векторы
vector{AM} (x;y;z); vector{AB} (0;0;1) и vector{AС1}(1;1;1)
компланарны (лежат в одной плоскости).
Записываем условие компланарности векторов: определитель третьего порядка, составленный из координат этих векторов равен 0.
Раскрываем этот определитель и получаем уравнение плоскости ABC1:
x-y=0
vector{n2}(1;-1;0)

cos φ=|1-1+0|/(sqrt(2)*sqrt(3))=0/(sqrt(2)*sqrt(3))=0

φ= π/2

3б)
Cоставляем уравнение плоскости AB1С( cм. пункт 2б):
х+y-z=0
vector{n1}(1;1;-1)
Cоставляем уравнение плоскости A1BС1:
Пусть M (х;у;z) - произвольная точка этой плоскости.
Векторы
vector{A1M} (x;y-1;z-1); vector{A1B} (0;-1;1) и vector{A1С1}(1;0;1)
компланарны (лежат в одной плоскости).
Записываем условие компланарности векторов: определитель третьего порядка, составленный из координат этих векторов равен 0.
Раскрываем этот определитель и получаем уравнение плоскости ABC1:
x-y-z-2=0
vector{n2}(1;-1;-1)

cos φ=|1-1+1|/(sqrt(3)*sqrt(3))=1/(sqrt(3)*sqrt(3))=1/3

φ= arccos(1/3)

3в)
Cоставляем уравнение плоскости D1AС
Пусть M (х;у;z) - произвольная точка этой плоскости.
Векторы
vector{AM} (x;y;z); vector{AD1} (1;1;0) и vector{AC}(1;0;-1)
компланарны (лежат в одной плоскости).
Записываем условие компланарности векторов: определитель третьего порядка, составленный из координат этих векторов равен 0.
Раскрываем этот определитель и получаем уравнение плоскостиD1AC:
x-y+z-1=0
vector{n1}(1;-1;1)
Cоставляем уравнение плоскости B1AС
Пусть M (х;у;z) - произвольная точка этой плоскости.
Векторы
vector{AM} (x;y;z); vector{AB1} (0;-1;1) и vector{AC}(1;0;1)
компланарны (лежат в одной плоскости).
Записываем условие компланарности векторов: определитель третьего порядка, составленный из координат этих векторов равен 0.
Раскрываем этот определитель и получаем уравнение плоскостиD1AC:
x-z=0
vector{n2}(1;0;-1)

cos φ =|1+0-1|/(sqrt(2)*sqrt(3))=0/(sqrt(2)*sqrt(3))=0

φ= π/2