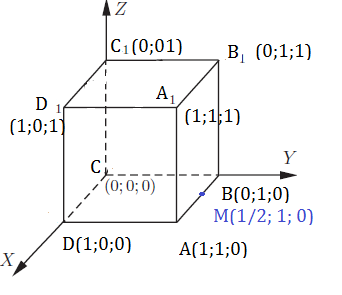
Задача 16046 В системе координат Оxyz расположен куб...
Условие
1. До прямой АС1 от точки:
а) А1;
б) В1;
в) С.
2. До плоскости А1ВС1 от точки:
а) В1;
б) С;
в) D1;
г) D.
3. Между прямыми:
а) А1С1 и АB1;
б) BD1 и В1C
в) BD и В1М, где М — середина ребра АВ.
Решение
1a)
vector{C1A1} (1;1;0)
vector{C1A} (1;1;-1)
vector{C1A1}* vector{C1A}=1*1+1*1+0*(-1)=2
|vector{C1A1}|=sqrt(2)
|vector{C1A}|=sqrt(3)
cos∠A1C1A=2/(sqrt(2)*sqrt(3))=sqrt(2/3)
sin∠A1C1A=sqrt(1-(sqrt(2/3))^2)=1/sqrt(3)
d=|A1C1|*sin∠A1C1A=sqrt(2)*(1/sqrt(3))=sqrt(2/3).
1б)
vector{C1A} (1;1;-1)
vector{C1В} (0;1;-1)
vector{C1A}* vector{C1В}=1*0+1*1+(-1)*(-1)=2
|vector{C1A}|=sqrt(3)
|vector{C1В}|=sqrt(2)
cos∠AC1В=2/(sqrt(3)*sqrt(2))=sqrt(2/3)
sin∠AC1В=sqrt(1-(sqrt(2/3))^2)=1/sqrt(3)
d=|С1В|*sin∠AC1В=sqrt(2)*(1/sqrt(3))=sqrt(2/3).
1в)
vector{C1A} (1;1;-1)
vector{C1С} (0;0;-1)
vector{C1A}* vector{C1С}=1*0+1*0+(-1)*(-1)=1
|vector{C1С1}|=sqrt(1)=1
|vector{C1A}|=sqrt(3)
cos∠AC1С=1/(sqrt(3)*sqrt(1))=1/sqrt(3)
sin∠AC1С=sqrt(1-(1/sqrt(3))^2)=sqrt(2/3)
d=|СC1|*sin∠AC1С=1*(sqrt(2/3))=sqrt(2/3).
2а)
Пусть М(х;у;z)- произвольная точка плоскости А1ВС1
Тогда векторы
vector{MB}(x;y-1;z); vector{A1B}(1;0;1); vector{A1C}(1;1;0) компланарны ( лежат в одной плоскости).
Условие компланарности : определитель третьего порядка, составленный из координат указанных векторов равен 0.
Раскрываем определитель и получаем уравнение плоскости А1ВС1:
x-y-z+1=0
Расстояние от точки с координатами (х_(о);у_(о);z_(o)) находим по формуле
d=|x_(o)-y_(o)-z_(o)+1|/sqrt(3)d=|0
2a)
d=|0-1-1+1|/sqrt(3)=1/sqrt(3);
2б)
d=|0-0-0+1|/sqrt(3)=1/sqrt(3);
2в)
d=|1-0-1+1|/sqrt(3)=1/sqrt(3)
2г)
d=|1-0-0+1|/sqrt(3)=2/sqrt(3)
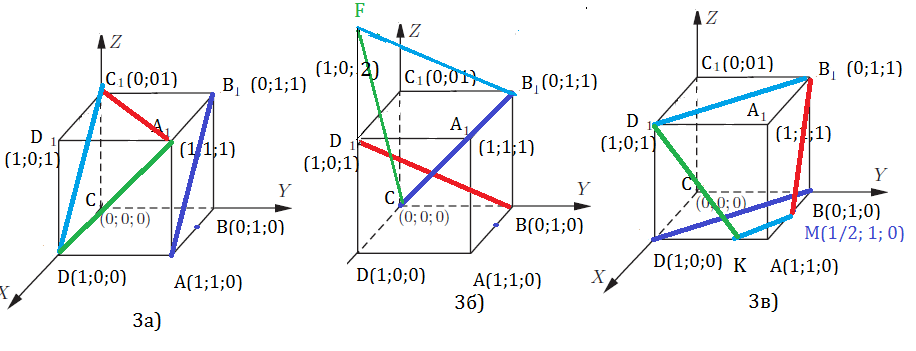
3 а)
Проводим D1C || AB1. Плоскость DC1A1 || AB1
Cоставляем уравнение плоскости DC1A1
Пусть Р(х;у;z) - произвольная точка этой плоскости.
Векторы
vector{DP} (x;y;z); vector{C1D} (1;0;-1) и vector{DA1}(0;1;1)
компланарны (лежат в одной плоскости).
Записываем условие компланарности векторов: определитель третьего порядка, составленный из координат этих векторов равен 0.
Раскрываем этот определитель и получаем уравнение плоскости DC1A1
x-y+z-1=0
расстояние от любой точки прямой АB1, например В1, и есть расстояние между прямыми.
cм формулу в п.2
d(В1)=|0-1+1-1|/sqrt(3)=1/sqrt(3)
3б)
Проводим B1F || BD1. Плоскость B1FC || BD1
Cоставляем уравнение плоскости B1FC
F(1;0;2)
Пусть Р(х;у;z) - произвольная точка этой плоскости.
Векторы
vector{CP} (x;y;z); vector{CB} (0;1;1) и vector{CF}(1;0;2)
компланарны (лежат в одной плоскости).
Записываем условие компланарности векторов: определитель третьего порядка, составленный из координат этих векторов равен 0.
Раскрываем этот определитель и получаем уравнение плоскости B1FC:
2x-y-z=0
расстояние от любой точки прямой BD1, например В, и есть расстояние между прямыми.
d(В)=|0-1-0|/sqrt(4+1+1)=1/sqrt(6)
3в)
Проводим МК || BD и B1D1||BD.
Плоскость MB1D1K || BD
Cоставляем уравнение плоскости MB1D1K
Пусть Р(х;у;z) - произвольная точка этой плоскости.
Векторы
vectorB1CP} (x;y-1;z-1); vector{B1M} (1/2;0;-1) и
vector{B1D1}(-1;1;0) - компланарны (лежат в одной плоскости).
Записываем условие компланарности векторов: определитель третьего порядка, составленный из координат этих векторов равен 0.
Раскрываем этот определитель и получаем уравнение плоскостиMB1D1K:
2x+2y+z-3=0
расстояние от любой точки прямой BD, например D, и есть расстояние между прямыми.
d(D)=|2+0+0-3|/sqrt(4+4+1)=1/3