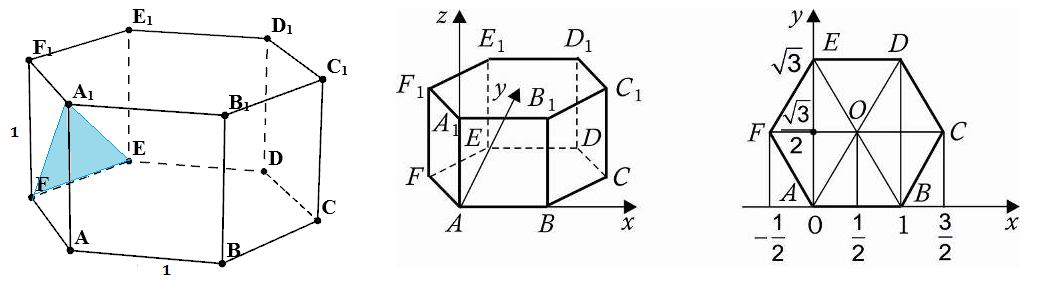
Задача 16027 В правильной шестиугольной призме...

slava191

25.05.2017

В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все ребра которой равны 1, найдите расстояние от точки В до плоскости A1EF.

SOVA

26.05.2017

★

Расстояние от точки В до плоскости A1EF найдем применяя метод координат.
(см. рисунок).
Введем систему координат так как показано на рисунке.
Тогда
F(-1/2; (sqrt(3))/2;0)
E(0;sqrt(3);0)
A1(0;0;1)
B(1;0;0)
Пусть М(х;у;z)- произвольная точка плоскости A1EF.
Тогда векторы
vector{A1M}, vector{A1E} и vector{FE} компланарны.
Что означает, что определитель третьего порядка составленный из координат этих векторов равен 0
(х;y;z-1)
(0;sqrt(3);-1}
(1/2;(sqrt(3))/2;0)
Уравнение плоскости А1EF:
sqrt(3)*x-y-sqrt(3)*z+sqrt(3)=0
Расстояние от точки B(1;0;0)
находим по известной формуле нахождения расстояния от точки до плоскости
d=|sqrt(3)+sqrt(3)|/sqrt(3+1+3)=2sqrt(3)/sqrt(7)
О т в е т. 2sqrt(3)/sqrt(7)=2sqrt(21)/7