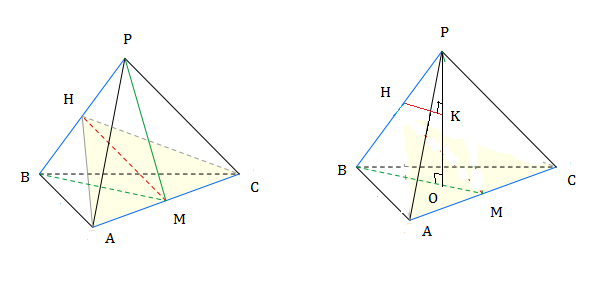
Задача 16026 Точка Н — середина ребра РВ правильного...

slava191

25.05.2017

Точка Н — середина ребра РВ правильного тетраэдра РАВС. Опустите перпендикуляр из точки H:

а) на прямую АС;
б) на высоту РО тетраэдра, О принадлежит (АВС).

Найдите длину каждого перпендикуляра, если ребро тетраэдра равно 2sqrt(2) .

SOVA

26.05.2017

★

а) Пусть М- середина АС.
Покажем, что МН - общий перпендикуляр к прямым РВ и АС.
АМ=МС
ВМ - медиана равностороннего треугольника АВС , а значит и высота.
ВМ ⊥ АС.

МН- медиана равнобедренного треугольника РМВ,
Значит МН и высота.
МН ⊥ РВ

ВМ=2sqrt(2)*(sqrt(3)/2)=sqrt(6)
ВН=РВ/2=(2sqrt(2))/2=sqrt(2)
По теореме Пифагора из прямоугольного треугольника
ВНМ
МН=sqrt((sqrt(6))^2-(sqrt(2))^2)=sqrt(6-2)=sqrt(4)=2
О т в е т. а)2.
б)
РО ⊥ пл. АВС ⇒∠РОВ=90 градусов
НК|| BO

НК- средняя линия треугольника РОВ
НК⊥ РО
НК=(1/2)ВО=(1/2)*(2sqrt(2))*((sqrt(3))/3)=(sqrt(6))/3
О т в е т. б) (sqrt(6))/3