Около выпуклого четырехугольника описана окружность радиуса 2. Одна из сторон этого четырехугольника равна 3. Найдите длину противоположной ей стороны четырехугольника, если его диагонали взаимно перпендикулярны.
математика 10-11 класс
15766
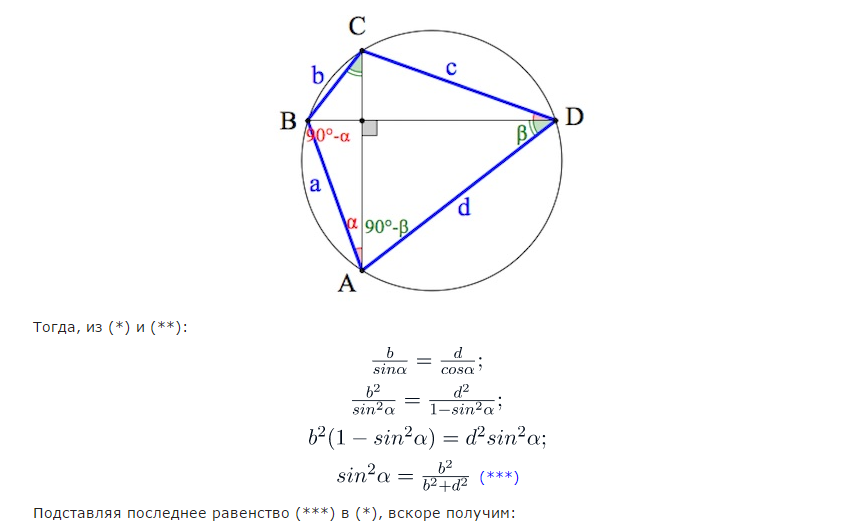
Если четырехугольник со взаимно перпендикулярными диагоналями вписан в окружность, то квадрат диаметра этой окружности равен сумме квадратов противоположных сторон.
(см. доказательство этого факта в приложении)
(2R)^2=b^2+d^2
R=2
b=3
d^2=(2R)^2-b^2=4^2-3^2=7
d=sqrt(7)

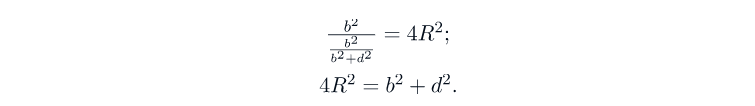
Вопросы к решению (1)
почему b=7, если в условии задачи говорится, что одна из сторон этого четырехугольника равна 3?
опечатка, в вычислении d использовано b=3