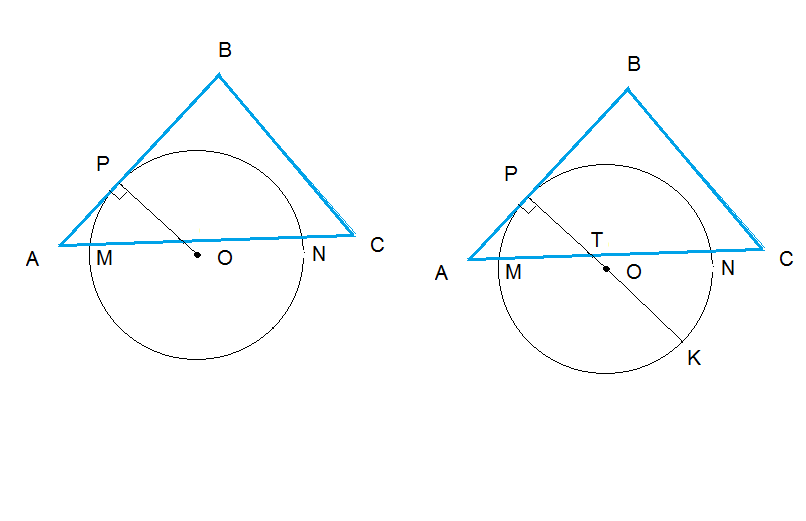
Задача 15957 Точки M и N лежат на стороне АС...

slava191

22.05.2017

Точки M и N лежат на стороне АС треугольника АВС на расстояниях соответственно 9 и 32 от вершины A. Найдите радиус окружности, проходящей через точки М и N и касающейся луча АВ, если cosBAC=2sqrt(2)/3

SOVA

23.05.2017

★

По свойству касательной и секущей, проведенных к окружности из одной точки:
АР^2=AM*AN
AP=sqrt(9*32)=12sqrt(2)
Продолжим РО до пересечения с окружностью в точке К.
РК- диаметр
РК=2R
Пусть РК пересекает АС в точке Т.
Из прямоугольного треугольника АРТ
сos∠РАТ=АР/АТ
∠РАТ=∠ВАС
2sqrt(2)/3=12sqrt(2)/AT⇒ АТ=18
По теореме Пифагора
PT^2=AT^2-AP^2=18^2-(12sqrt(2))^2=324-288=36
PT=6
По свойству пересекающихся хорд
МТ*TN=PT*TK
MT=AT-AM=18-9=9
TN=AN-AT=32-18=14
9*14=6*TK
TK=21
PK=PT+TK=6+21=27
PK=2R
2R=27
R=13,5
О т в е т. 13,5