Задача 15903 Постройте график функции...

slava191

20.05.2017

Постройте график функции [m]y=1-\frac{x+5}{x^2+5x}[/m] и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.

SOVA

21.05.2017

★

Область определения функции:
х^2+5x ≠ 0
x≠0; x≠-5

y=1-(x+5)/(x*(x+5));
y=1-(1/x)
Cтроим график
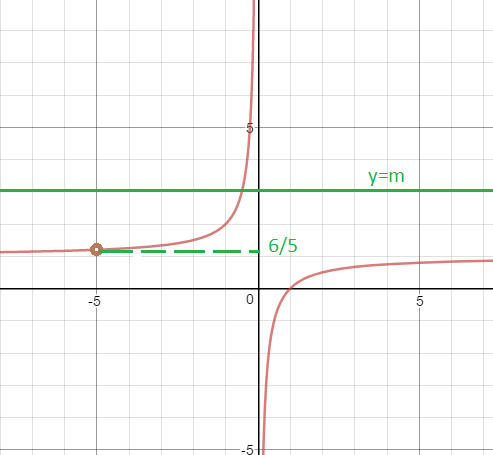
y=1-(1/x) (это гипербола) на области определения данной функции, поэтому на графике выколота точка х=-5 у=6/5.
Гипербола у=-1/х не принимает значения у=0
Гипербола у=1-(1/х) не принимает значения у=1

Прямые у=6/5 и у=1 не имеют с графиком общих точек
О т в е т. 1; 6/5