Задача 15632 Иррациональное уравнение ...
Условие
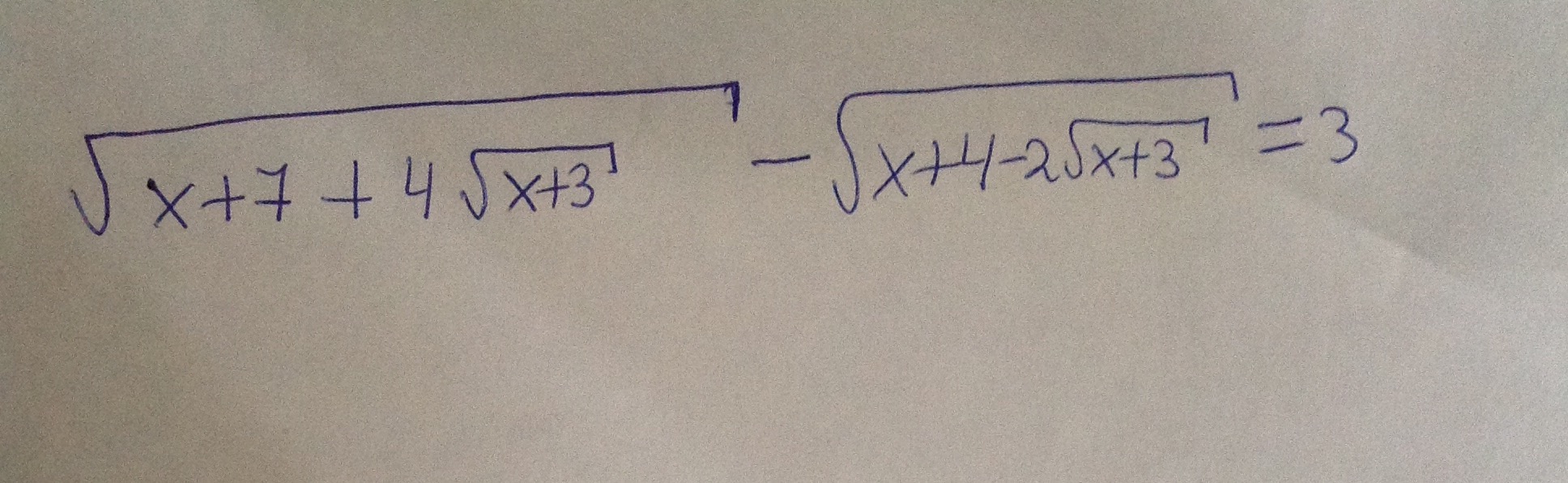
Решение
|sqrt(x+3)+2|-|sqrt(x+3)-1|=3
При х больше или равно -3
sqrt(x+3)+2 > 0,
|sqrt(x+3)+2|=sqrt(x+3)+2
Если
sqrt(x+3)-1 больше или равно 0,
sqrt(x+3) больше или равно 1,
х+3 больше или равно 1,
х больше или равно -2
то
|sqrt(x+3)-1|=sqrt(x+3)-1
Уравнение принимает вид
sqrt(x+3)+2-sqrt(x+3)+1=3
верно при всех х, таких что
{x больше или равно -3;
{x больше или равно -2
Значит [-2;+ бесконечность) - решение уравнения
Если
sqrt(x+3)-1 < 0,
sqrt(x+3) < 1,
0 меньше или равно х+3 < 1,
-3 меньше или равно х < -2
то
|sqrt(x+3)-1|=-sqrt(x+3)+1
Уравнение принимает вид
sqrt(x+3)+2+sqrt(x+3)-1=3
2sqrt(x+3)=2
sqrt(x+3)=1
x+3=1
x=-2 не удовл. условию
-3 меньше или равно х < -2
во втором случае уравнение не имеет корней.
О т в е т. [-2;+ бесконечность)