Задача 15609 Постройте график функции y=(1/2)(|x/5,5...

slava191

07.05.2017

Постройте график функции y=(1/2)(|x/5,5 - 5,5/x| + x/5,5 + 5,5/x) и определите, при каких значениях m прямая у = m имеет с графиком ровно одну общую точку.

SOVA

07.05.2017

★

Если
1)(x/5,5) – (5,5/x) больше или равно 0, то
|(x/5,5) – (5,5/x)|=(x/5,5) – (5,5/x)
y=(1/2)*(2x/5,5)=x/5,5

(x/5,5) – (5,5/x) больше или равно 0
(x^2-(5,5)^2)/(5,5*x) больше или равно 0

решаем неравенство методом интервалов:
_-__ [-5,5] __+__ (0) ___-__ [5,5] ___+__

Строим график у=х/5,5 при
x∈[-5,5;0)U[5,5;+бесконечность)

2)1)(x/5,5) – (5,5/x) < 0, то
|(x/5,5) – (5,5/x)|=-(x/5,5) + (5,5/x)
y=(1/2)*(2*5,5)/(x)=5,5/x

(x/5,5) – (5,5/x) < 0
(x^2-(5,5)^2)/(5,5*x) < 0

решаем неравенство методом интервалов:
_-__ (-5,5) __+__ (0) ___-__ (5,5) ___+__

Строим график у=5,5/x при
x∈(-бесконечность;-5,5)U(0;5,5)

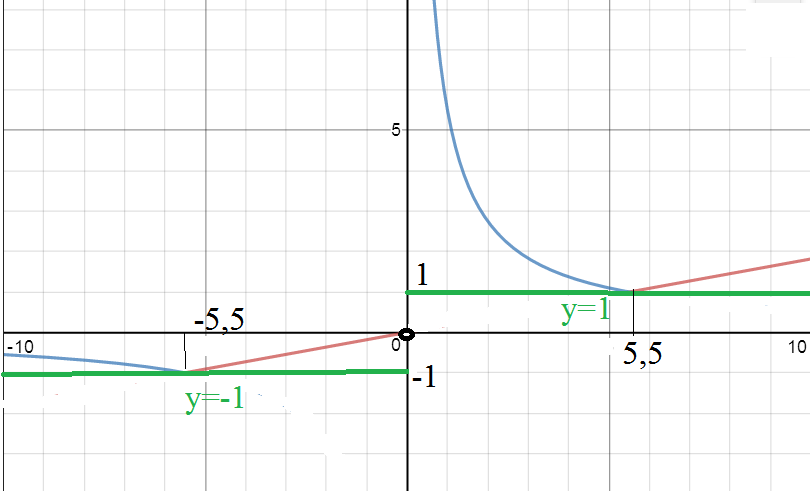
Cм. рисунок

О т в е т. m=-1 или m=1