Задача 15385 В правильной треугольной пирамиде SABC с...

u955916103

28.04.2017

В правильной треугольной пирамиде SABC с вершиной S сторога основания равна 9,а ребра 12.на ребре AC взята точка L, на ребре AB точка M, на ребре AS точка K. CL=BM=SK=3.найдите площадь сечения LMK

SOVA

28.04.2017

★

Треугольник ALM подобен треугольнику АВС.
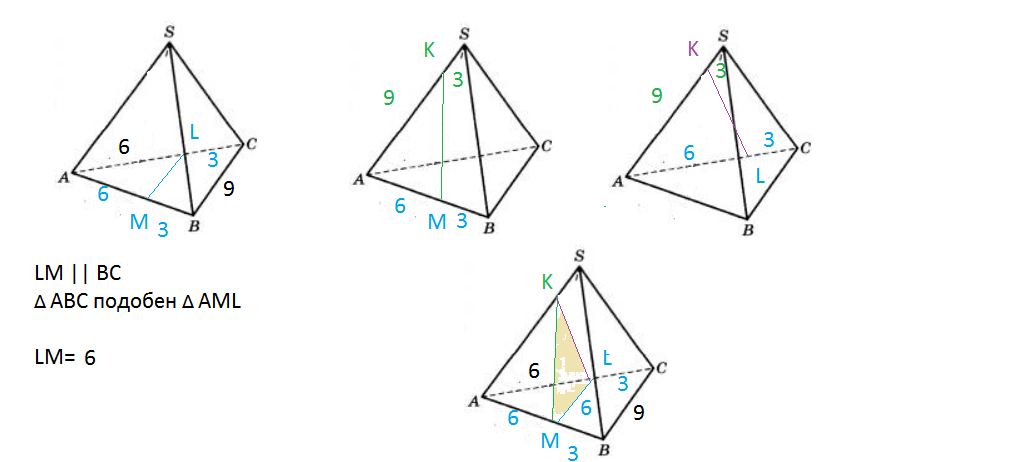
АВС- равносторонний со стороной 9, ALM - равносторонний со стороной 6.
LM=6

Треугольники SAB, SBC, SAC равны между собой.
Это равнобедренные треугольники, боковые стороны
SA=SB=SC=12
Основания
AB=BC=AC=9
сos∠SAB=4,5/12=3/8
По теореме косинусов
KM^2=AK^2+AM^2-2*AK*KM*cos∠SAB=
=9^2+6^2-2*9*6*(3/8)=81+36-(81/2)=(81/2)+36=153/2
KM=(sqrt(306))/2
KM=KL=(sqrt(306))/2

Cечение KML - равнобедренный треугольник.
Найдем высоту этого треугольника по теореме Пифагора:
h^2=KM^2-(ML/2)^2=(306/4)-3^2=(306-36)/4=
=270/4=135/2
h=sqrt(135/2)
S( Δ KML) =(1/2)ML*h=(1/2)*6*sqrt(135/2)=9*(sqrt(30))/2