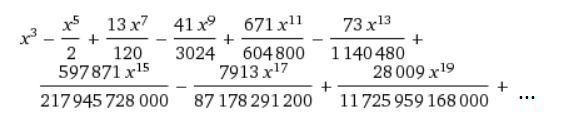Задача 15371 Разложить по степеням x функцию sin^3x и...

slava191

27 апреля 2017 г.

Разложить по степеням x функцию sin³x и исследовать сходимость разложения

SOVA

27 апреля 2017 г.

★

Применяем формулу:
sin³x=(1/4)·(3sinx–sin3x)=(3/4)sinx–(1/4)sin3x

Так как
sinx=x–(x³/3!)+(x⁵/5!)–(x⁷/7!)+...
...+ (–1)^n–1·x^2n–1/(2n–1)! + ...
Ряд сходится на (–∞; + ∞)

Тогда
sin3x=(3x)–((3x)³/3!)+((3x)⁵/5!)–((3x)⁷/7!)+...
... + (–1)^n–1·(3x)^2n–1/(2n–1)! + ...
Ряд сходится на (–∞; + ∞)

sin³x=(3/4)·(x–(x³/3!)+(x⁵/5!)–(x⁷/7!)+...
... + (–1)^n–1·x^2n–1/(2n–1)! + ...)–
–(1/4)·((3x)–((3x)³/3!)+((3x)⁵/5!)–((3x)⁷/7!)+...
...+ (–1)^n–1·(3x)^2n–1/(2n–1)! + ...)=

=(3/4)x–(3/4)x +((–3x³)/(4·3!)+(3³x³)/(4·3!))+

+((3x⁵)/(4·5!)–(3⁵x⁵)/(4·5!))+...

...+(–1)^2n–1(3–3^2n–1)x^2n–1/4·(2n–1)!+ ...

=
cм. приложение.
Ряд сходится на ( – ∞; + ∞) как разность двух сходящихся рядов.