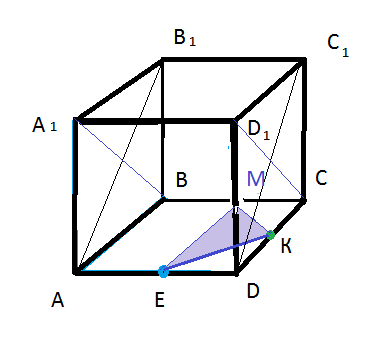
Задача 15193 Точки E и K -соответственно середины...

u4621621654

21.04.2017

Точки E и K -соответственно середины ребер AD и DC куба ABCDA1B1C1D1. Постройте сечение куба плоскостью, которая проходит через прямую KE и перпендикулярна плоскости ADC1. Вычислить периметр этого сечения, если длина ребра куба равна 2 см.

SOVA

21.04.2017

★

Плоскость ADC1 это плоскость ADB1C1.

Пл. ADB1C1 ∩ пл. DCC1D1 = C1D.
Проводим KM ⊥ C1D,
так как диагонали квадрата DCC1D1 взаимно перпендикулярны, то КM|| CD1.
KM ⊥ пл.DCC1D1, так как КМ перпендикулярна двум пересекающимся прямым этой плоскости.
КM ⊥ C1D
и
КM ⊥AD ( AD ⊥ пл. DCC1D1, а значит перпендикулярна любой прямой, лежащей в этой плоскости, в том числе и прямой КМ).

КМ - средняя линия Δ DCD1
КЕ - средняя линия Δ АСD
МЕ - средняя линия Δ ADD1

Равносторонний треугольник ЕКМ - искомое сечение
КМ=КЕ=МЕ=(1/2)АС=(1/2)*2sqrt(2)=sqrt(2)
Р( сечения)=3sqrt(2).
О т в е т. 3sqrt(2).