Задача 15179 log(x-5)(2x+3)^(sqrt(16-x) меньше или...
Условие
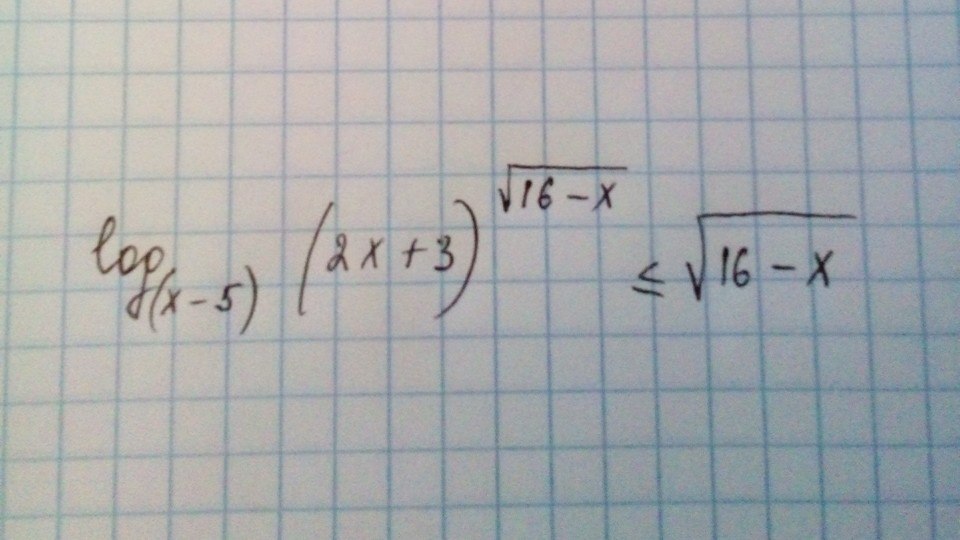
Решение
{x-5 > 0 ⇒ x > 5;
{x-5≠ 1 ⇒ x≠ 6;
{2x+3 > 0 ⇒ x > -1,5
{16-x больше или равно 0 ⇒ x меньше или равно 16
ОДЗ: х∈ (5;6)U(6;16]
По свойству логарифма степени:
log_(a)b^k=klog_(a) b, a > 0, b > 0, a≠1
sqrt(16-x)*(log_(x-5)(2x+3) -1) меньше или равно 0
Неравенство нестрогое.
Произведение двух множителей равно 0, когда хотя бы один из множителей равен 0, а второй при этом не теряет смысла.
Поэтому
sqrt(16-x)=0
x=16
при х=16
log_(16-5)(2*16+3)-1 не теряет смысла
Поэтому первый ответ х=16
Так как sqrt(16-x) больше или равно 0 при любом х из ОДЗ, т. е.
при х∈ (5;6)U(6;16], данное неравенство примет вид:
log_(x-5)(2x+3) меньше или равно 1
1=log_(x-5)(x-5)
Применяем метод рационализации логарифмических неравенств:
(х-5-1)*(2х+3-х-5) меньше или равно 0
(x-6)*(x-2) меньше или равно 0
2 меньше или равно x меньше или равно 6
C учетом ОДЗ получаем второй ответ (5;6)
Объединяя оба ответа
окончательный ответ
(5;6)U{16}.