Задача 15107 log2x + 5sqrt(log2x) + 15 ......
Условие
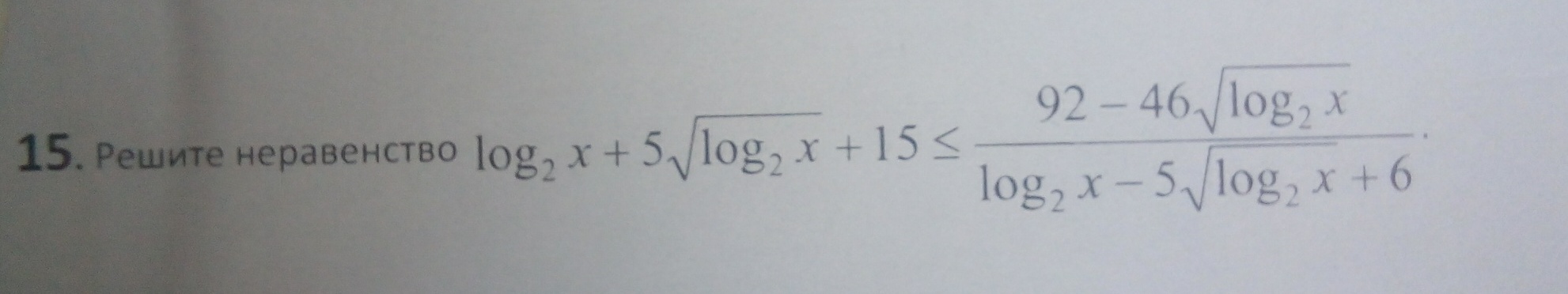
Решение
{x > 0;
{log_(2)x > 0⇒x > 1
{log_(2)x-5sqrt(log_(2)x)+6≠0⇒
log_(2)x≠2;log_(2)x≠3⇒x≠4;x≠8
ОДЗ:(1;4)U(4;8)U(8;+бесконечность)
Замена переменной:
sqrt(log_(2)x)=t
log_(2)x=t^2
Неравенство принимает вид:
t^2+5t+15 меньше или равно (92-46t)/(t^2-5t+6);
t^2+5t+15 меньше или равно 46 (2-t)/(t-2)(t-3);
t^2+5t+15 меньше или равно (-46 /(t-3));
t^2+5t+15 + (46 /(t-3))меньше или равно 0;
(t^3+5t^2+15t-3t^2-15t-45+46)/(t-3)) меньше или равно 0;
(t^3+2t^2+1)/(t-3) меньше или равно 0;
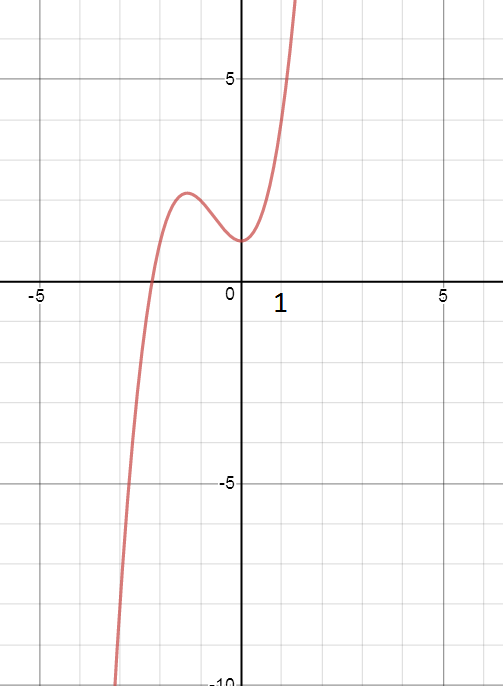
y=t^3+2t^2+1 возрастает на ОДЗ, так как y`=3t^2+4t > 0 при t > 1
cм. график функции y=t^3+2t^2+1 на рисунке.
Значит решением неравенства является
t-3 < 0
t < 3
Возвращаемся к переменной х:
sqrt(log_(2)x) < 3.
0 меньше или равно log_(2)x < 9;
1 меньше или равно x < 2^9=512
C учетом ОДЗ получаем ответ
(1;4)U(4;8)U(8;512)