Задача 14931 Исследовать функцию и построить ее...

Partnerservis1

10.04.2017

Исследовать функцию и построить ее график.
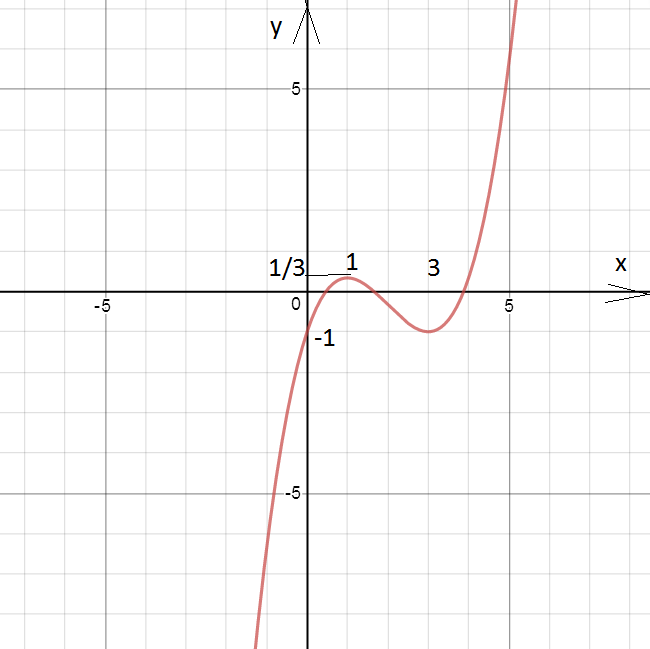
F(x)=1/3x3-2x2+3x-1

SOVA

11.04.2017

★

F`(x)=x^2-4x+3
F`(x)=0
x^2-4x+3=0
D=16-12=4
x1=(4-2)/2=1 или х2=(4+2)/2=3 - точки возможного экстремума.
Исследуем знак производной
F`(10)=10^2-4*10+3 > 0

__+_ (1) __-__ (3) ___+__

На (- ∞;1) и (3;+∞) функция возрастает
На (1;3) убывает

x=1 - точка максимума, производная меняет знак
с + на -
у(1)=(1/3)-2+3-1=(1/3)
х=3 - точка минимума, производная меняет знак
с - на +
у(3)=(1/3)*3^3-2*3^2+3*3-1=9-18+9-1=-1
Строим график