Задача 14765 ...

u1765933157

4 мая 2017 г. в 00:00

Решите уравнение (5cosx – 3) / (3tgx + 4) = 0

Найдите все корни этого уравнения, принадлежащие отрезку [2π, 7π/2]

SOVA

4 июня 2017 г. в 00:00

★

Дробь равна нулю если числитель равен нулю, а знаменатель отличен от нуля.
{cosx=3/5 ⇒ х= ±arccos (3/5) + 2πk, k∈Z ;
{tgx≠–4/3 ⇒ х ≠ arctg(–4/3)+πn, n∈Z .

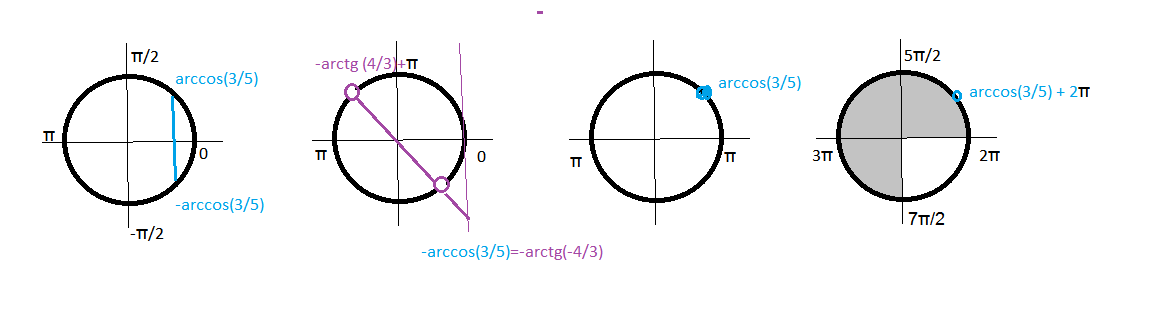
если cosx=3/5, то sinx=√1–cos²x=√1–(3/5)²=
=√16/25=±4/5
Угол, косинус которого равен 3/5, синус равен 4/5 расположен в первой четверти.
Угол, косинус которого равен 3/5, синус равен (–4/5) расположен в четвертой четверти. Тангенс этого угла
равен (–4/5):(3/5)=–4/3
Этот угол не входит в ОДЗ (иначе знаменатель обращается в 0)
Cм рисунок

О т в е т.
а) arccos (3/5) + 2πk, k∈Z
б)arccos(3/5) + 2π