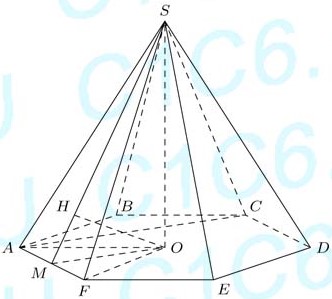
Задача 14651 В правильной шестиугольной пирамиде...

u3796163

02.04.2017

В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите синус угла между прямой BC и плоскостью SAF.

vk373384374

03.04.2017

★

точка О-центр основания,точка М-середина ребра AF,ОН-высота треугольника MSO.
Диагональ правильного шестиугольника АС-перпендикулярна его стороне AF.
Из прямоугольного треугольника ASO получаем
SO=корень SА^2-AO^2=корень 2^-1^2=корень из 3
Из прямоугольного треугольника АОМ получаем
МО=АО^-AM^=корень из 3/2
MSO
SM=MO^2+SO^2=корень из 15/2
sinУгла SMO=MO/SM=корень из 3/корень из 15=1/корень из 5=корень из 5/5
Ответ:корень из 5/5.