Задача 14645 ...
Условие
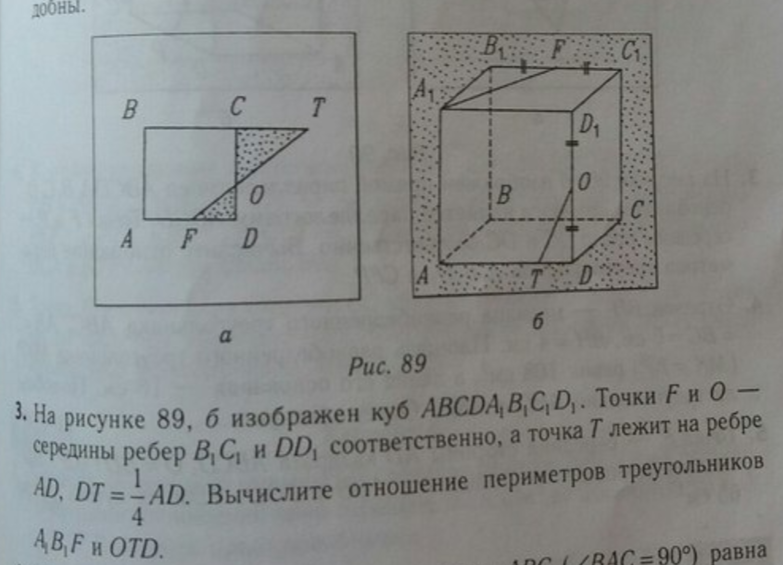
предмет не задан
679
Решение
★
Тогда B1F=2a;
TD=a
По теореме Пифагора из прямоугольного треугольника А1В1F:
A1F=sqrt((4a)^2+(2a)^2)=sqrt(20a^2)=2sqrt(5)*a
По теореме Пифагора из прямоугольного треугольника TOD:
OT=sqrt((a)^2+(2a)^2)=sqrt(5a^2)=sqrt(5)*a
Р( Δ А1В1F)=A1B1+B1F+A1F=4a+2a+2asqrt(5)=
=(6+2sqrt(5))a
Р( Δ TOD)=TD+DO+OT=a+2a+asqrt(5)=
=(3+sqrt(5))a
Р( Δ А1В1F):Р( Δ TOD) = 2 : 1