Задача 14636 ...

slava191

01.04.2017

2. На рисунке 93, б изображен прямоугольный параллелепипед
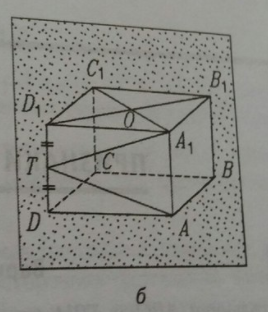
ABCDA1B1C1D1. Точка Т — середина ребра DD1, точка О — точка
пересечения диагоналей грани A1B1C1D1. Известно, что ∠B1OA1 = 60°
и 2B1A1 = AA1. Вычислите отношение периметров треугольников
B1OA1 и A1TA.

SOVA

01.04.2017

★

Пусть А1В1=х, тогда АА1=2х.
Диагонали прямоугольника равны и в точке пересечения делятся пополам, значит ОА1=B1O=D1O=C1O

Δ A1OB1 - равнобедренный (А1О=В1О) и угол В1ОА1 равен 60 градусов, значит Δ A1OB1 - равносторонний.

ОА1=B1O=D1O=C1O=х

Δ D1OA1 - равнобедренный (D1О=A1О) и угол D1ОА1 равен 180 градусов -60 градусов=120 градусов.

D1A1=sqrt(3)x

Из прямоугольного треугольника D1TA1
(D1T=(1/2)AA1=(1/2)*2x=x) по теореме Пифагора:
TA1=sqrt(x^2+(sqrt(3)x)^2=sqrt(4x^2)=2x

Δ A1TA- равносторонний

Р(ΔВ1ОА1):Р(Δ A1TA)=А1В1:А1А-х:2х=1:2