Задача 14635 Все на картинке...
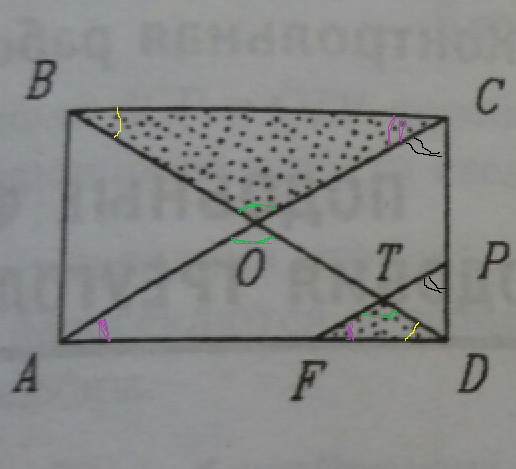
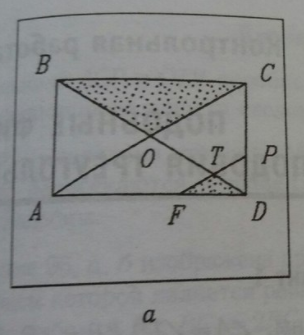
Условие
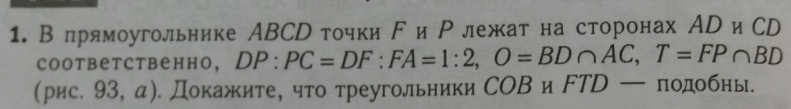
предмет не задан
628
Решение
★
FP|| AC
Значит,
∠ACD=∠FPD
∠CAD=∠PFD
как соответственные углы при параллельных прямых.
∠CAD=∠АСВ внутренние накрест лежащие, значит
∠АСВ=∠PFD
∠CВD=∠FDT внутренние накрест лежащие
Δ СОВ и Δ FDT подобны по двум углам.