Задача 14479 2^(6-5x/2)-2^(7-2x)-2^(-x/2-1)+1 /...
Условие
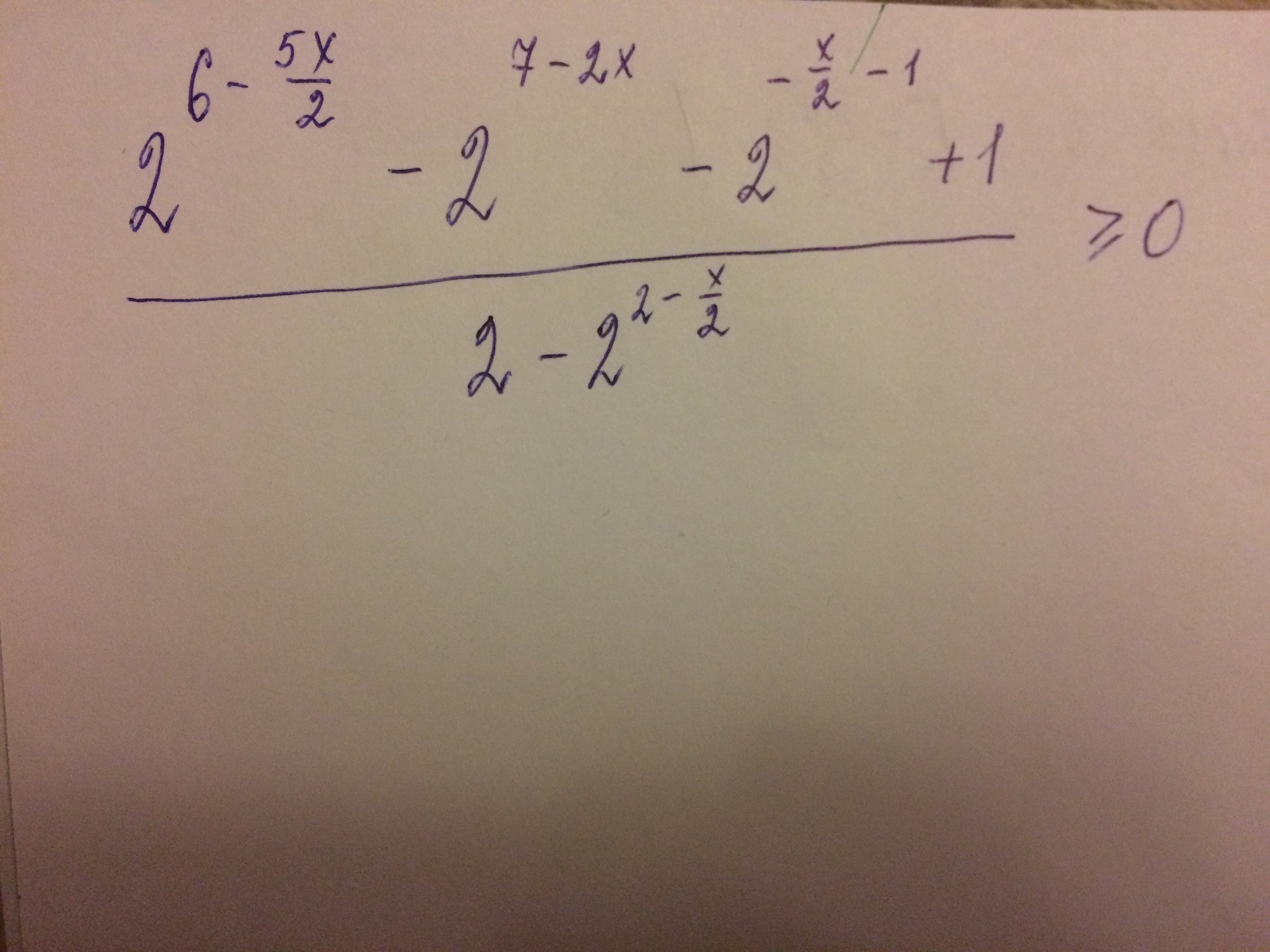
Решение
2^(7-2x)=2^7*2^(-x/2)^4
2^((-x/2)-1)=2^(-x/2)*2^(-1)
2^(2-(x/2))=2^2*2^(-x/2)
Замена переменной
2^(x/2)=t
t > 0
(64t^5-128t^4-(1/2)t+1)/(2-4t) больше или равно 0
(128t^5-256t^4-t+2)/(2-4t) больше или равно 0
(t-2)(128t^4-1)/(2-4t)больше или равно 0
Применяем метод интервалов.
Нули числителя:
(t-2)(128t^4-1)=0
t=2 или t=2^(-7/4) или t=-2^(-7/4)
__-_ [-2^(-7/4)] _+_ [2^(-7/4)] _-__ (1/2) _+_ [2] __-__
C учетом t > 0 получаем ответ.
0 < t≤2^(-7/4); (1/2) < t≤2
0 < 2^(-x/2)≤2^(-7/4); 2^(-1) < 2^(-x/2)≤2
(-x/2) ≤ (-7/4); (-1) < (-x/2)≤1.
x ≥ 3,5 ; -2 ≤ x < 2
О т в е т. [-2; 2) U [3,5; + бесконечность)
