Задача 14123 Задание 1 и 2 с подробным решением)...
Условие
с подробным решением)
математика 10-11 класс
1155
Решение
★
=2(x^6+(3/x^4)-8)*(x^6+(3/x^4)-8)`=
=2(x^6+(3/x^4)-8)*(6x^5+(3*(-4)/x^5).
2.
Область определения (-бесконечность; + бесконечность)
у`=3x^2-12x
y`=0
3x^2-12x=0
3x*(x-4)=0
x=0 и х=4 - точки возможного экстремума.
Применяем достаточное условие экстремума.
Определяем знак производной
__+__ (0) ___-_____ (4) __+__
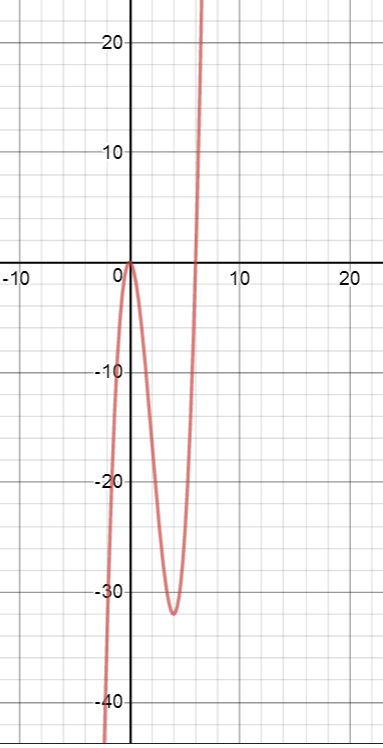
На (- бесконечность;0) функция возрастает, на (0;4) убывает, на (4;+бесконечность) возрастает.
х=0- точка локального максимума
у(0)=0
х=4- точка локального минимума
у(4)=4^3-6*4^2=-32